Точка приложения силы давления жидкости на плоские стенки.

Представим на рисунок 2.5 деталь предыдущего чертежа. Центр давления силы 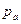будет совпадать с центром тяжести фигуры, так как поверхностное давление 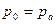, передаваясь через жидкость, равномерно распределяется по рассматриваемой площади. Что касается избыточного давления, то оно распределяется неравномерно по площади фигуры: чем глубже расположена точка фигуры, тем большее давление она испытывает; поэтому центр давления силы 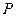будет лежать ниже центра тяжести фигуры (см. точку ).

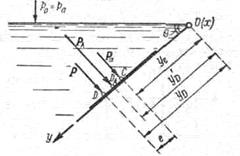
Искомая сила Р_А является геометрической суммой сил Р_а и Р. Точка D_A будет лежать между точками С и D; эта точка D_A найдется в результате геометрического сложения сил Р_а и Р. Таким образом, вопрос сводится к отысканию точки D, определяемой координатой у_D. Зная у_D, мы далее, как указано выше, найдем и величину у_D, определяющую положение точки D_A.

Расчетную зависимость для величины у_D находят, исходя из следующего условия: сумма моментов составляющих элементарных сил pdS относительно оси Ох равна моменту равнодействующей силы Р относительно той же оси Ох.

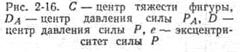
Рисунок 2.8 - - Расчёт центра давления

Имея в виду это условие, можем написать:

.

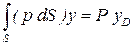(2.55)

Эту формулу можно переписать в виде

.

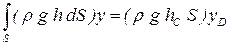(2.56)

или

.

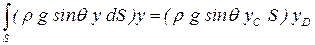(2.57)

Откуда

.

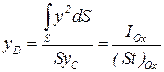(2.58)

где

.

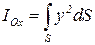(2.59)

момент инерции плоской фигуры относительно оси Ох, а

.

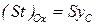(2.60)

есть, как это уже отмечалось, статический момент плоской фигуры относительно осиОх,

Формулу (2.41) можно еще переписать в виде

.

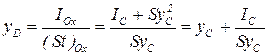(2.61)

или

.

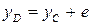(2.62)

где положительная величина е называется эксцентриситетом. Эксцентриситет

.

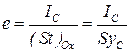(2.63)

причем здесьl_C есть момент инерции рассматриваемой плоской фигуры относительно горизонтальной оси, проходящей через центр тяжести фигуры. Как видно, центр давления силы Р лежит ниже центра тяжести фигуры на величину, равную е.

Выше мы ограничились отысканием только одной координаты точки D (координаты yD). Однако в общем случае приходится еще определять и вторую координату (хD). Ее можно найти, исходя из уравнения моментов соответствующих сил (уравнения, аналогичного (2-86)) относительно оси Оу.

<567891011>

---

Дата добавления: 2016-04-06; просмотров: 928;

---