Прямой скачок уплотнения

Явление разрывного (скачкообразного) изменения параметров газового потока при переходе через некоторую поверхность называется ударной волной. Если поверхность разрыва представляет собой неподвижную плоскость, нормальную к скорости равномерного потока газа, то такое явление называется прямым скачком уплотнения. Скачки уплотнения могут возникать только в сверхзвуковом потоке газа, они сопровождаются уменьшением скорости и возрастанием давления, плотности и температуры. Критическая скорость и температура торможения при переходе через скачок не изменяются.

Основная система уравнений, описывающих прямой скачок уплотнения, состоит:

из уравнения неразрывности

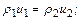(12.31)

уравнения импульса (количества движения)

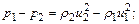(12.32)

уравнения энергии (уравнения Бернулли)

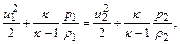(12.33)

где индексами 1 и 2 отмечены значения параметров потока соответственно перед скачком и после него.

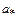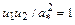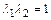Исключая из этой системы давления и плотности и вводя в рассмотрение критическую скорость , получаем формулу Прандтля или , из которой следует, что скорость перед скачком должна быть сверхзвуковой, а за скачком - дозвуковой.

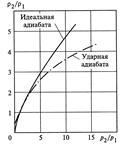
Рис.12.4. Сравнение идеальной и ударной адиабат

Исключая скорост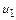и и 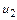из основной системы уравнений, получаем уравнение ударной адиабаты (адиабаты Гюгонио)

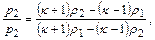(12.34)

график которой и сопоставление с идеальной адиабатой Пуассона 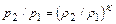приведены на рис.12.4.

Использовав эти графики, можно показать, что переход через прямой скачок уплотнения является неизоэнтропным процессом и сопровождается возрастанием энтропии; образование скачка разрежения невозможно; уплотнение в прямом скачке не может превосходить

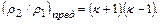(12.35)

Изменение параметров газового потока при переходе через прямой скачок определяются формулами:

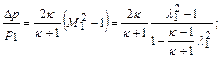(12.36)

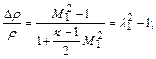(12.37)

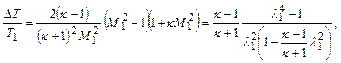(12.38)

где ; ; .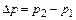

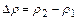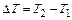Потеря механической энергии в скачке оценивается отношением полных давлений (давлений торможения) за скачком и перед ним:

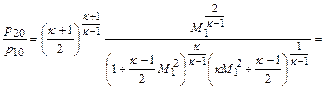
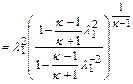. (12.39)