Истечение газа через сопло

При истечении невязкого газа через прошлифованное сужающееся сопло с равномерным распределением скоростей на срезе скорость истечения определяется по формуле Сен-Венана - Ванцеля

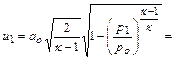
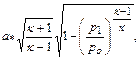(12.40)

где 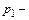давление во внешней среде.

Массовый расход

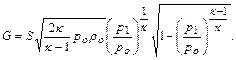(12.41)

а его максимальное значение

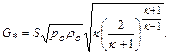(12.42)

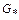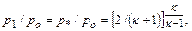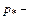Расход достигается при где давление на срезе сопла, соответствующее критической скорости 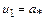. Значение 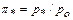называется критическим отношением давлений. Формулы дают реальные расходы пр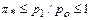и и 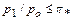соответственно.

Для получения практически равномерного распределения скоростей в выходном сечении сопла его профиль должен быть очерчен по кривой Витошинского, определяемой уравнением

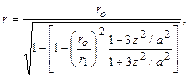(12.43)

где 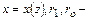радиусы соответственно промежуточного, входного и выходного поперечных сечений сопла; 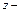координата, отсчитываемая вдоль оси сопла ( 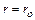при ).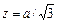

Значения 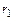и 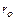выбираются из конструктивных условий, параметр 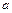принимают обычно равным 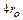. Профиль Витошинского пригоден для соединения труб различных диаметров при дозвуковых скоростях вплоть до 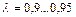. Сопла, присоединяемые к резервуарам, могут очерчиваться по дугам окружностей, лемнискатам или параболам.

При истечении реального (вязкого) газа через сужающееся сопло имеют место потери энергии вследствие внутреннего трения. Для оценки пропускной способности сопла вводится коэффициент расхода 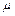, определяемый как отношение истинного расхода газа к теоретическому (изоэнтропному).

Расчетная формула для расхода принимает вид

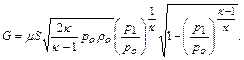(12.44)

Согласно опытам, проведенным в МЭИ, для сопла лемнискатного профиля коэффициенты расхода составляют 0,95…0,98, возрастая с увеличением числа Рейнольдса, которое в опытах изменялось в пределах 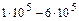. С увеличением отношения давлений 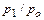коэффициент расхода несколько уменьшается. Для конических сопл при различных углах конусности значения могут уменьшаться вплоть до 0,65.

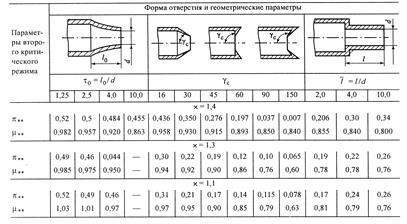
Таблица 12.1

Второе критическое отношение давлений 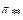и коэффициенты расхода

для сопл различных форм

Вследствие влияния сил вязкости и образования пограничного слоя на поверхности сопла структура течения не вполне соответствует теоретической. Это проявляется и в том, что значение относительного давления 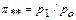, при котором достигается максимальный расход, оказывается меньше теоретического 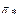. Значение 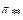возрастает с увеличением числа Re* и убывает с увеличением длины сопла при соблюдении условия 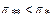. В табл.12.1 приведены значения 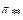для различных сопл и соответствующие коэффициенты расхода.

Для получения сверхзвуковых скоростей истечения необходимо применение сопла Лаваля (рис.12.3). Элементарный расчет такого сопла, основанный на одномерной теории, состоит в определении площадей минимального (критического) сечения S* и выходного сечения 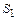(рис.12.3). Заданными считаются массовый расход 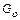параметры торможения и скорость на выходе 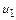. Полагая 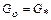площадь S* определяем по формуле:

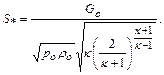(12.45)

Выходное сечение рассчитывают исходя из уравнения неразрывности

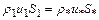
или

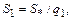(12.46)

где

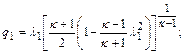
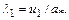(12.47)

Форма расширяющейся части сопла в первом приближении может быть принята конической.

Такое сопло может обеспечить лишь приближенное к заданному среднее значение скорости на выходе, но создает неравномерное распределение местных скоростей.

Большей равномерности скоростей на выходе можно достигнуть, если задать закон изменения скорости вдоль оси сопла 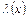и определить промежуточные сечения по формуле

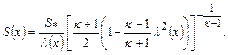(12.48)

Для получения равномерного распределения скоростей профиль расширяющейся части сопла должен быть рассчитан методами теории двумерных течений. Кроме того, должно учитываться влияние вязкости; с этой целью разработаны приближенные методы.