В трубе постоянного сечения
Расчетная система уравнений одномерного потока вязкого газа без энергообмена с внешней средой включает в себя:
уравнение неразрывности
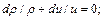 (12.49)
(12.49)
уравнение состояния
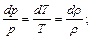 (12.50)
(12.50)
уравнение энергии (Бернулли)
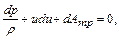 (12.51)
(12.51)
где 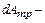 работа сил вязкости (потери), отнесенные к единице массы в движущемся газе.
работа сил вязкости (потери), отнесенные к единице массы в движущемся газе.
Поскольку данное течение энергетически изолировано, температура и энтальпия торможения, а также критическая скорость постоянны ( 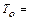 const,
const, 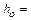 const,
const, 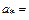 const). С учетом этого из предыдущей системы можно получить
const). С учетом этого из предыдущей системы можно получить
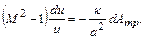 (12.52)
(12.52)
Поскольку всегда 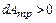 , дозвуковой поток (М<1) под влиянием трения ускоряется (
, дозвуковой поток (М<1) под влиянием трения ускоряется ( 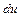 >0), а сверхзвуковой (М>1) тормозится (
>0), а сверхзвуковой (М>1) тормозится ( 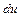 <0). Непрерывный переход через скорость звука под влиянием только трения невозможен.
<0). Непрерывный переход через скорость звука под влиянием только трения невозможен.
Соотношение между параметрами газового потока в двух сечениях трубы выражаются формулами:
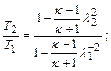 (12.53)
(12.53)
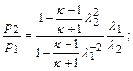 (12.54)
(12.54)
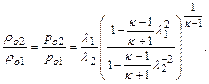 (12.55)
(12.55)
Работа сил трения на участке трубы длиной может быть приближенно выражена гидравлической зависимостью Вейсбаха - Дарси
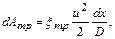 (12.56)
(12.56)
где 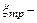 гидравлический коэффициент трения, зависящий от числа Рейнольдса, как и для несжимаемой жидкости;
гидравлический коэффициент трения, зависящий от числа Рейнольдса, как и для несжимаемой жидкости; 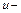 средняя скорость;
средняя скорость; 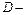 диаметр трубы. Здесь для коэффициента трения употреблено обозначение
диаметр трубы. Здесь для коэффициента трения употреблено обозначение 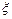 , для отличия его от безразмерной скорости
, для отличия его от безразмерной скорости 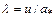 .
.
Используя эту зависимость, уравнение можно привести к виду
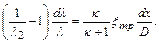 (12.57)
(12.57)
Полагая 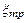 =const (что допустимо ввиду малого изменения числа Re по длине трубы), в результате интегрирования можно получить
=const (что допустимо ввиду малого изменения числа Re по длине трубы), в результате интегрирования можно получить
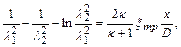 (12.58)
(12.58)
где 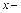 расстояние между начальным сечением
расстояние между начальным сечением 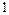 и расчетным сечением трубы 2. Обозначая
и расчетным сечением трубы 2. Обозначая
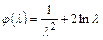 (12.59)
(12.59)
и определяя приведенную длину трубы как
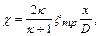 (12.60)
(12.60)
уравнение представляем в форме
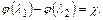 (12.61)
(12.61)
Так как при 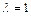 функция
функция 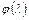 достигает минимума
достигает минимума 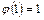 , то при заданном
, то при заданном 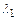 и
и 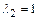 достигается некоторая критическая максимальная приведенная длина трубы
достигается некоторая критическая максимальная приведенная длина трубы
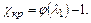 (12.62)
(12.62)
Зависимость 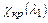 показана на рис.12.5. При заданных
показана на рис.12.5. При заданных 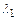 и длине трубы критическая скорость может быть достигнута в конце трубы.
и длине трубы критическая скорость может быть достигнута в конце трубы.
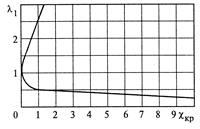
Рис.12.5. Зависимость приведенной критической длины трубы 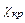
от начальной скорости 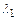
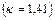
Скорость дозвукового потока на входе в трубу заданной приведенной длины не может превышать значения, определяемого уравнением
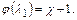 (12.63)
(12.63)
Если 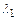 < 1и заданное значение приведенной длины трубы
< 1и заданное значение приведенной длины трубы 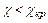 , то на выходе
, то на выходе 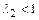 . Если же
. Если же 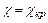 то
то 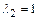 . При
. При 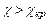 реализация заданного значения
реализация заданного значения 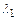 в начале трубы невозможна.
в начале трубы невозможна.
Если поток на входе в трубу сверхзвуковой ( 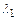 >1) и приведенная длина
>1) и приведенная длина 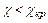 , то
, то 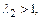 т.е. на выходе из трубы поток сохранится сверхзвуковым (однако
т.е. на выходе из трубы поток сохранится сверхзвуковым (однако 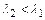 ). При
). При 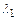 >1 и
>1 и 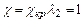 . Когда при
. Когда при 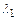 >1 задано
>1 задано 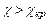 некотором сечении трубы возникает скачок уплотнения, за которым устанавливается дозвуковой ускоренный поток.
некотором сечении трубы возникает скачок уплотнения, за которым устанавливается дозвуковой ускоренный поток.
Положение скачка, предполагая его прямым, определяем следующим образом. Скорости перед скачком 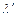 и за ним
и за ним 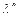 связаны формулой Прандтля
связаны формулой Прандтля
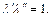
В то же время 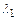 связана с координатой скачка
связана с координатой скачка 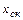 уравнением
уравнением
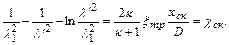 (12.64)
(12.64)
С учетом того, что 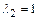 , можно написать
, можно написать
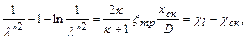 (12.65)
(12.65)
где 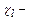 приведенная длина трубы, откуда
приведенная длина трубы, откуда
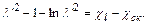 (12.66)
(12.66)
Решая совместно два последних уравнения, находим 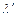 и
и 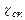 .
.
Для обеспечения заданного значения 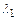 на входе в трубу заданной приведенной длины требуется вполне определенный перепад давлений между входным и выходным сечениями.
на входе в трубу заданной приведенной длины требуется вполне определенный перепад давлений между входным и выходным сечениями.
Если 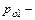 полное давление во входном сечении, а
полное давление во входном сечении, а 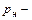 давление в среде, в которую газ вытекает из трубы, то значение
давление в среде, в которую газ вытекает из трубы, то значение 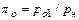 , называемое располагаемым отношением давлений, будет определяться массовый расход и другие параметры газа в данной трубе. Если на выходе из трубы устанавливается критическая скорость (
, называемое располагаемым отношением давлений, будет определяться массовый расход и другие параметры газа в данной трубе. Если на выходе из трубы устанавливается критическая скорость ( 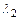 =1), то соответствующее отношение давлений называется критическим:
=1), то соответствующее отношение давлений называется критическим:
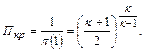 (12.67)
(12.67)
При заданном располагаемом отношении давлений расчет истечений через трубу заданных размеров производят по следующей схеме. Выражая расход во входном сечении через полное давление 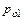 в выходном сечении через статическое давление, получаем
в выходном сечении через статическое давление, получаем
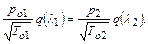 (12.68)
(12.68)
Ввиду адиабатности течения 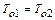 и, следовательно,
и, следовательно,
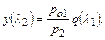 (12.69)
(12.69)
Если 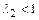 , то
, то 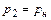 или
или
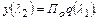 (12.70)
(12.70)
Скорости 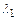 и
и 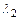 связаны уравнением
связаны уравнением
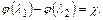 (12.71)
(12.71)
Отсюда находятся скорости 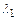 и
и 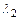 как функции заданных величин
как функции заданных величин 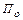 и
и 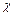 . Приведенные уравнения справедливы при
. Приведенные уравнения справедливы при 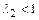 . Минимальное значение
. Минимальное значение 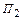 , при котором
, при котором 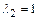 , определяют по уравнению
, определяют по уравнению
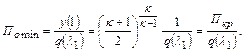 (12.71)
(12.71)
При значениях 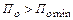 на выходе из трубы
на выходе из трубы
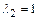 и
и 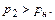 (12.72)
(12.72)
Дата добавления: 2016-02-16; просмотров: 1614;
