Косые скачки уплотнения

При торможении сверхзвукового потока могут возникать поверхности разрыва, которые наклонены к вектору скорости под углом, отличным от прямого. Такие разрывы называются косыми скачками уплотнения (рис.12.8). Расчетная система уравнений косого скачка включает в себя уравнения:

неразрывности

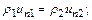(12.101)

количества движения (импульса) в проекции на нормаль к фронту скачка

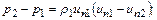(12.102)

количества движения в проекции на направление, параллельное фронту скачка,

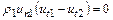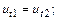или (12.103)

энергии

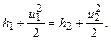(12.104)

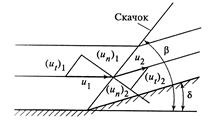
Рис.12.8. Расчетная схема косого скачка уплотнения

Из этой системы выводятся соотношения между параметрами потока за скачком и перед ним:

для отношения давлений

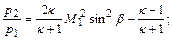(12.105)

отношения плотностей

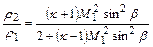; (12.106)

отношения температур

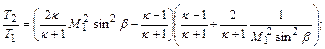(12.107)

отношения давлений торможения

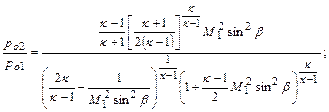(12.108)

разности значений энтропии

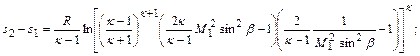(12.109)

Последняя формула показывает, что переход через косой скачок не является изоэнтропийным и сопровождается потерями механической энергии.

Связь между углом наклона фронта скачка 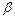и углом поворота потока в скачке 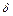определяется формулой

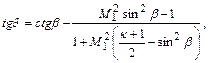(12.110)

из которой следует, что кривая 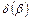имеет максимум, т.е. существует угол наклона скачка 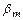, соответствующий максимально возможному отклонению потока в скачке 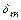. Значения 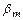определяются из уравнения

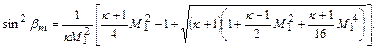
(12.111)

Кроме того, каждому значению 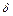отвечают два значения 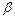. Скорость потока за скачком 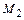связана со скоростью 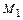перед скачком соотношением

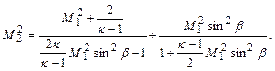(12.112)

откуда следует, что для каждого значения 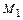существует некоторое значение 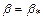, при котором 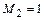. При 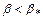поток за скачком остается сверхзвуковым (слабые скачки), при 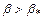он будет дозвуковым (сильные скачки). Для определения 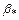служит уравнение

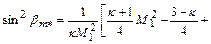
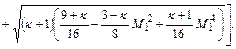(12.113)

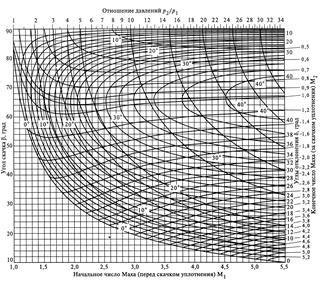
Рис.12.9. Расчетная диаграмма косых скачков уплотнения

Номограмма для расчета параметров косых скачков приведена на рис.12.8.