Газодинамические функции
Если газовый поток с местными параметрами 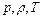 изоэнтропно затормозить, то полученные параметры
изоэнтропно затормозить, то полученные параметры 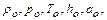 будут иметь смысл местных параметров торможения, а приведенные формулы будут выражать местные связи между безразмерными величинами.
будут иметь смысл местных параметров торможения, а приведенные формулы будут выражать местные связи между безразмерными величинами.
Помимо функций
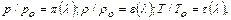 (12.17)
(12.17)
представленных на рис.12.1, употребительны также другие газодинамические функции. Например, использовав функцию приведенного расхода газа,
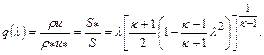 (12.18)
(12.18)
можно рассчитать массовый расход газа через сечение 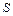
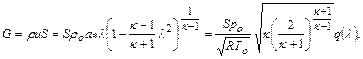 (12.19)
(12.19)
где сомножитель 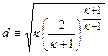 имеет следующие значения:
имеет следующие значения:
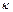
| 1,40 | 1,35 | 1,33 | 1,30 | 1,25 |
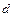
| 0,685 | 0,676 | 0,673 | 0,667 | 0,658 |
Использовав функцию
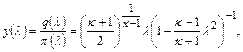 (12.20)
(12.20)
для массового расхода газа можно получить следующее выражение:
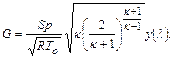 (12.21)
(12.21)
Графики функций 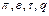 для
для 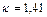 приведены на рис.12.1.
приведены на рис.12.1.
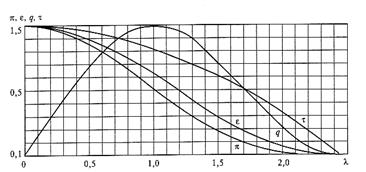
Рис.12.1. Графики газодинамических функций 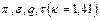
Функции 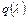 и
и 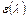 связаны соотношением
связаны соотношением 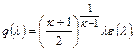 (12.22)
(12.22)
При использовании уравнения импульса газа вводится понятие полного импульса, которое может быть выражено в следующих видах:
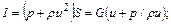 (12.23)
(12.23)
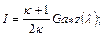 (12.24)
(12.24)
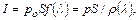 (12.25)
(12.25)
где 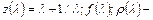 газодинамические функции, определяемые формулами
газодинамические функции, определяемые формулами
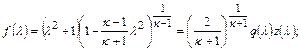 (12.26)
(12.26)
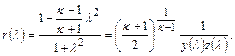 (12.27)
(12.27)
Графическое представление газодинамических функций и дано на рис.12.2. Более точные, чем по этим графикам, значения функций можно получить с помощью таблиц, приводимых в руководствах по газовой динамике.
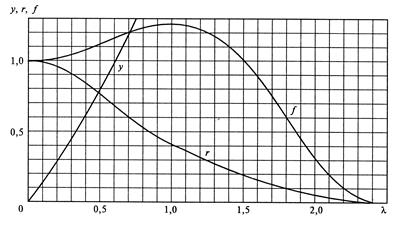
Рис.12.2. Графики газодинамических функций 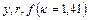
Дата добавления: 2016-02-16; просмотров: 2097;
