ТЕХНИЧЕСКИХ УСТРОЙСТВ В ПРОГРАММЕ EXCEL

Для цепи переменного тока, показанной на рис. 3.25, построим

выведенные ранее частотные

характеристики

по формулам (3.33),

(3.34), (3.35) в околорезонансной области.

Введём исходные данные так же, как в прошлой задаче в массив ячеек A1-F1 (рис. 3.26).

В ячейку B3 введём частоту 40 Гц, в ячейку B4 введём 41 Гц, шаг по частоте составит 1 Гц. Выделим массив B3-B4. Мышкой протянем

его до ячейки B115.

В ячейке A3 рассчитаем круговую частоту от частоты, записанной в ячейке B3 (рис. 3.41). Выделим ячейку A3 и протянем выделение до

ячейки A115. Получим массив переменных.

Постоим фазочастотную характеристику по формуле (3.33).

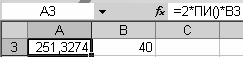
Рис. 3.41

В ячейку C3 внесем формулу (3.33):

=ATAN((A3*$C$1-$E$1*A3/($E$1*$E$1*A3*A3+1/$F$1/$F$1))/

/($D$1+(1/$F$1)/($E$1*$E$1*A3*A3+1/$F$1/$F$1)))*180/ПИ().

Следует обратить внимание на использование знака $ для обозна-

чения глобальных и локальных переменных (рис. 3.42).

Рис. 3.42

Выделим ячейку C3 и продолжим выделение с помощью мышки до ячейки С115. Выделим массив B3-C115. Вызовем «Мастер диа- грамм». Выберем для построения точечную диаграмму со сглаживаю- щими линиями. Поставим линии сетки по обеим осям. Выберем тип за- ливки «Прозрачная», подпишем оси и получим диаграмму фазочастот- ной характеристики (рис. 3.43).

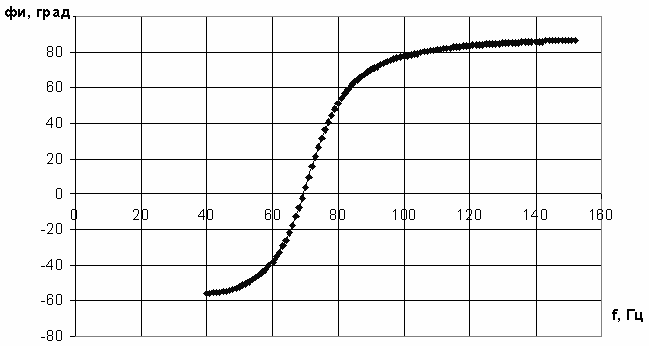
Рис. 3.43

Построим амплитудно-частотную характеристику по выражению

(3.34).

В ячейку D3 введём формулу (3.34):

=КОРЕНЬ(($D$1+($E$1^2*A3^2+1/$F$1^2)/$F$1)^2+(A3*$C$1-

$E$1*A3/($E$1^2*A3^2+1/$F$1^2))^2).

Выделим ячейку D3 и продолжим выделение до ячейки D115.

Итак, готов массив функции модуля комплексного сопротивления нагрузки. Построим его график по методике, описанной для фазоча- стотной характеристики (рис. 3.44).

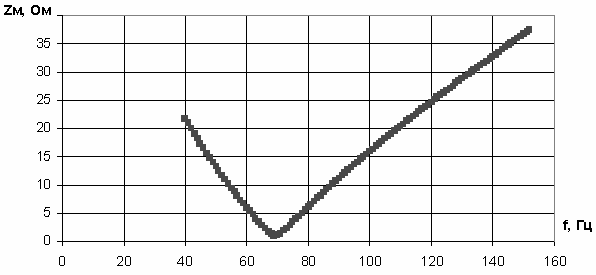
Рис. 3.44

Как видно из графика (рис. 3.44), функция имеет резонансный минимум в диапазоне частот от 60 до 80 Гц.

В столбце E разместим массив, рассчитанный по выражению

(3.35). В ячейку E3 поместим соответствующую формулу (рис. 3.45).

Рис. 3.45

Выделим ячейку E3 и продолжим выделение до E115. Получим массив значений для коэффициента мощности и построим его график (рис. 3.46).

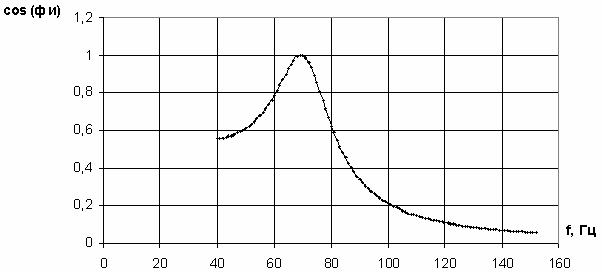
Рис. 3.46

На резонансной частоте коэффициент мощности равен 1.

ГЛАВА 5.