Мого тока, активной мощности и коэффициента мощности
Пусть к источнику переменного тока подключена активно-
реактивная нагрузка (рис. 3.25).
i1(t) L R1
U (t) =Um⋅sin(ω ⋅t)
C
i3(t)
R2
i2(t)
 Рис. 3.25
Рис. 3.25
Необходимо с применением программы Excel определить фазу потребляемого тока, активную мощность и коэффициент мощности на- грузки в установившемся режиме.
Ток через конденсатор пропорционален производной напряжения
du(t)
C⋅ C = i
(t). (3.24)
dt 3
Применим к выражению (3.24) прямое преобразование Лапласа и получим
C ⋅ p ⋅UC( p ) = I3 ( p ). (3.25)
Реактивное сопротивление конденсатора в операторной форме
| C |
I3 ( p)
1
C ⋅ p
. (3.26)
Реактивное сопротивление конденсатора в комплексной форме
| C |
I3 ( j ⋅ω)
1
C ⋅ j ⋅ω
= − j ⋅
1
C ⋅ω
, (3.27)
где ω = 2⋅π ⋅ f
– круговая частота гармонического входного напряжения,
f– частота гармонического входного напряжения.
В данной задаче примем частоту
f= 50 Гц , что соответствует час-
тоте промышленной электрической сети.
Проводимость конденсатора в комплексной форме
YC( j⋅ω) = C⋅ j⋅ω. (3.28)
Проводимость конденсатора Cи резистора R2
| CR2 R . |
Сопротивление конденсатора Cи резистора R2
ZCR2 ( j ⋅ω ) =
C⋅ j⋅ω+ 1
R2
. (3.30)
Полное сопротивление нагрузки
ZΣ( j ⋅ ω ) = R1 +
j ⋅ ω ⋅ L +
C⋅ j⋅ω+ 1 .
R2
(3.31)
Преобразуем (3.31), выделив явно действительную и мнимую час-
ти
ZΣ( j ⋅ω ) = R1 +
j ⋅ ω ⋅ L +
(3.32)
+ R2
− C ⋅ j ⋅ω
=
⎛ 1 + C⋅ j⋅ω⎞⋅⎛ 1
−C⋅ j⋅ω⎞
⎜ ⎟ ⎜ ⎟
⎝ R2
⎠ ⎝ R2 ⎠
= R1 +
j ⋅ω ⋅ L +
1 −C⋅ j⋅ω
R2 =
| R |
1 ⎛ ⎞
= R+ R2
⎜
+ j⋅⎜ω⋅ L−
C⋅ω ⎟
⎟.
1 1 1
+ C2 ⋅ω2
⎜ + C2 ⋅ω2 ⎟
| R |
| R |
2 ⎝ 2 ⎠
Так как фаза напряжения источника принимается равной нулю, то фаза тока нагрузки определяется по комплексному сопротивлению на- грузки (3.32)
ϕ (ω ) = arctg
ω ⋅ L −
C ⋅ ω
| R |
2
1 .
(3.33)
R1 +
R2
| R |
2 ⋅ω2
(3.32)
Модуль комплексного
сопротивления нагрузки определим из
⎜ ⎟ ⎜ ⋅ ⎟
| M |
⎜ R+
R2 ⎟
+ ⎜ω⋅ L− Cω ⎟
(3.34)
1 + C2 ⋅ω2 ⎟ .
⎜ R2
⎟ ⎜ R2 ⎟
⎝ 2 ⎠ ⎝ 2 ⎠
Коэффициент мощности активно-реактивной нагрузки
ξ (ω ) = cosϕ (ω ). (3.35)
Активная мощность нагрузки
P(ω) =
U2
⋅cosϕ(ω) =
( )
U ⋅ξ(ω), (3.36)
( )
ZM ω
ZM ω
где UД
– действующее значение напряжения источника.
Для численного решения задачи в Excel зададимся следующими параметрами:
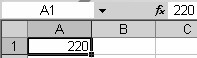
UД = 220 В – введём в ячейку A1 (рис. 3.26, а);
ω = 2 ⋅π ⋅ 50
рад/с – введём в ячейку B1 (рис. 3.26, б);
L1 = 0.05 Гн – введём в ячейку C1 (рис. 3.26, в);
R1 = 1 Ом
– введём в ячейку D1 (рис. 3.26, г);
Ф – введём в ячейку E1 (рис. 3.26, в);
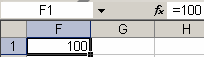
R2 = 100 Ом
– введём в ячейку F1 (рис. 3.26, е).


 а) б)
а) б)
в) г)

д) е)
Рис. 3.26
Согласно (3.29) в ячейке A3 рассчитаем проводимость конденса-
тора Cи резистора
R2 . Для этого воспользуемся функцией КОМ-
ПЛЕКСН из категории «Инженерные» (рис. 3.27).
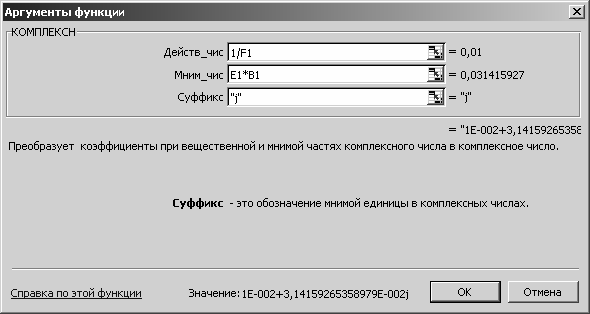
Рис. 3.27
Содержимое ячейки A3 представлено (рис. 3.28).

Рис. 3.28
В ячейке A4 согласно (3.30) рассчитаем сопротивление конденса-
тора Cи резистора
R2 . Воспользуемся функцией МНИМ.ДЕЛ для де-
ления на комплексное число (рис. 3.29).
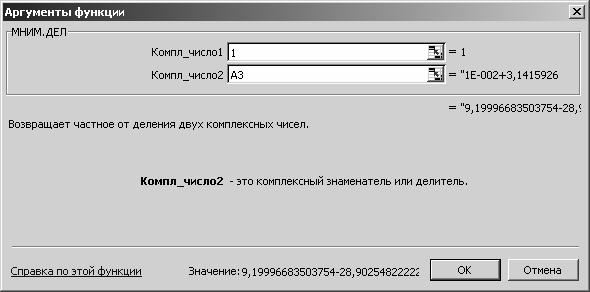
Рис. 3.29
Содержимое ячейки A4 представлено (рис. 3.30).

Рис. 3.30
Согласно
(3.31)
рассчитаем полное сопротивление
нагрузки.
Для
этого в ячейку A5 введём комплексное число
R1 + j ⋅ ω ⋅ L
(рис. 3.31).

Рис. 3.31
Затем в ячейке A6 необходимо произвести
сложение двух ком-
плексных чисел, находящихся в ячейках A4 и A5. Для этого воспользу-
емся функцией МНИМ.СУММ из категории «Инженерные» (рис. 3.32).
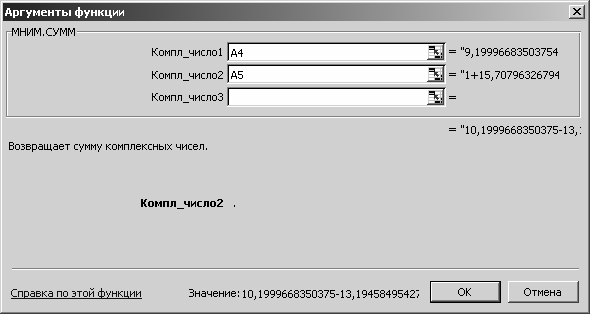
Рис. 3.32
Величина полного комплексного сопротивления нагрузки нахо-
дится в ячейке A6 (рис. 3.33).

Рис. 3.33
Определим в ячейке A7 угол сдвига фазы тока относительно гар-
монического входного напряжения, выраженный в радианах. Восполь-
зуемся
функцией МНИМ.АРГУМЕНТ из
категории «Инженерные»
(рис. 3.34).
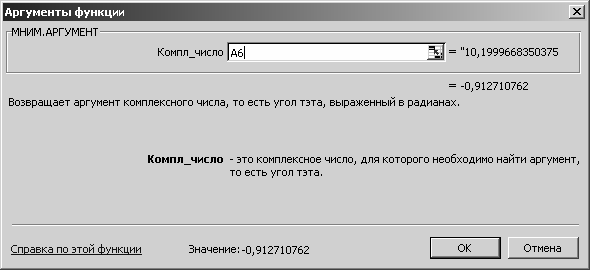 Рис. 3.34
Рис. 3.34
Содержимое ячейки A7 показано на рис. 3.35.

Рис. 3.35
Представим в ячейке A8 предыдущий полученный результат в градусах (рис. 3.36).
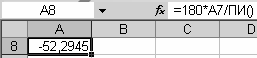
Рис. 3.36
В ячейке A9 определим коэффициент мощности (рис. 3.37).

Рис. 3.37
В ячейке A10 определим модуль комплексного сопротивления на-
грузки.
Для
этого
воспользуемся
функцией МНИМ.ABSиз категории
«Инженерные» (рис. 3.38).
 Рис. 3.38
Рис. 3.38
На рис. 3.39 показано содержимое ячейки A10.

Рис. 3.39
Определим активную мощность нагрузки (рис. 3.40).

Рис. 3.40
Полученные в данной главе результаты сведём в табл. 3.1.
Таблица 3.1
| Величина | Значение | Размерность |
| φ | -52,2945 | град |
| ξ | 0,611603 | - |
| P | 1774,951 | Вт |
Процедура расчёта, приведённая в данной главе, применима ко всем линейным цепям переменного тока.
ГЛАВА 4.
ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЭЛЕКТРО-
Дата добавления: 2016-04-02; просмотров: 620;
