Расчёт методом Эйлера переходного процесса заряда RC-цепи при коммутации на источник постоянного тока

Конденсатор ёмкостью C через резистор R подключается к источ- нику постоянного тока с ЭДС E. До коммутации конденсатор был раз- ряжен. Рассчитать методом Эйлера переходный процесс заряда конден- сатора и определить время переходного процесса. Переходный процесс заканчивается, когда конденсатор зарядится на 95% от установившегося значения.

Дифференциальное уравнение для послекоммутационной цепи выглядит, как

dU= E−U

(3.37)

dt С ⋅ R,

где U – напряжение на конденсаторе,

t– время.

В качестве индексной переменной выберем переменную j.

На нулевом шаге имеем исходные данные

t0 = 0,

U0 = 0. (3.38)

Согласно методу Эйлера на шаге расчёта j+1 имеем следующие соотношения

⎧t j+1 = t j+ ∆t

⎪

⎨ −

(3.39)

⎪Uj+1

⎩

=Uj

E U ,

+ ∆t ⋅ j

С ⋅ R

где ∆t

– шаг интегрирования, определяемый как

∆t= С ⋅ R.

(3.40)

Пусть

С = 0.001 Ф, R=1 Ом, E=100 В , тогда

∆t= 0.001⋅1 = 25⋅10−6 с.

В ячейку A1 введём начальное значение времени, в ячейку B1

введём начальное значение напряжения (рис. 3.47).

Рис. 3.47

В ячейку A2 введём

25 ⋅10−6. Выделим массив ячеек A1-A2 и с

помощью мышки продолжим выделение до ячейки A160. В ячейку B2

внесём формулу для расчёта напряжения (рис. 3.48).

Рис. 3.48

Выделим ячейку B2 и её

содержимое вставим в ячейку B3 с по-

мощью сочетания клавиш <Ctrl>+<C> (копировать) и <Ctrl>+<V> (вста- вить). Выделим массив B2-B3 и с помощью мышки продолжим выделе- ние до ячейки B160. Выделим массив A1-B160, вызовем «Мастер диа- грамм», выберем точечную диаграмму со значениями, соединёнными сглаживающими линиями, проставим линии сетки по обеим осям, выбе- рем обычный тип заливки, подпишем оси. На полученной диаграмме

курсором выделим график переходного процесса, найдём точку с коор-

динатой 95 В (рис. 3.49).

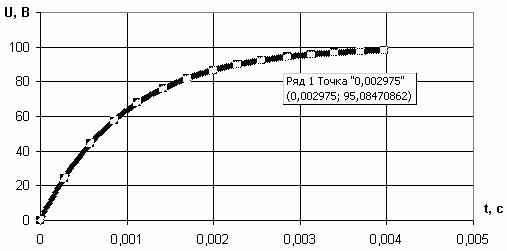
Рис. 3.49

Таким образом, время переходного процесса заряда конденсатора составляет 0.002975 с (рис. 3.49).