Расчёт методом Эйлера переходного процесса пуска вхолостую двигателя постоянного тока независимого возбуждения
Пусть двигатель постоянного тока с независимым возбуждением
(ДПТ с НВ) подключается к источнику постоянного тока U(рис. 3.50).








 Рис. 3.50
Рис. 3.50
Необходимо рассчитать переходный процесс пуска ДПТ с НВ при пуске вхолостую, определить величины броска тока якоря, наибольший противоток и перерегулирования по скорости в процентах. В начале пе- реходного процесса скорость и ток были равны нулю.
Якорная цепь ДПТ с НВ на схеме замещения (рис. 3.50) состоит
из:
R – суммарного сопротивления якорной цепи, L – суммарной индуктивности якорной цепи,
E – электродвижущей силы, пропорциональной скорости вала ω.
ЭДС ДПТ с НВ рассчитывается как
E= ω⋅c, (3.41)
где c – электромеханический коэффициент ДПТ с НВ.
Электромеханический коэффициент определяется как
c= UН − IН ⋅ R, (3.42)
ωН
где U Н , I Н , ωН
вала ДПТ с НВ.
– номинальные напряжение якоря, ток якоря и скорость
Система дифференциальных уравнений, описывающих процесс пуска ДПТ с НВ вхолостую, выглядит как
| U |
⎪ dt
⎨
+ ω ⋅ c
(3.43)
⎪I⋅c= J⋅ dω,
⎩⎪ dt
где J – момент инерции вала двигателя.
Явно выделим правые части дифференциальных уравнений
⎧dI
= U− I⋅ R−ω⋅c
⎪ dt L
⎨
(3.44)
⎪dω
= I⋅c.
⎪⎩ dt J
В качестве индексной переменной выберем переменную j.
На нулевом шаге имеем исходные данные
t0 = 0,
ω0 = 0, I0 = 0 . (3.45)
Согласно методу Эйлера на шаге расчёта j+1 имеем следующие соотношения
⎧
⎪tj+1 = tj+ ∆t
⎪
(3.46)
| I |
⎨ j+1
⎪
= I j
U− I⋅ R−ω⋅c
+ ∆t⋅ j j
L
⎪
⎪ωj+1
⎩
= ω j
I⋅c
+ ∆t⋅ j .
J
Шаг интегрирования рассчитаем следующим образом
J⋅ R⋅ L
| t . |
(3.47)
Зададимся численными параметрами для решения задачи в Excel
(см. табл. 3.2).
Таблица 3.2
| Величина | Значение | Размерность |
| U Н | В | |
| I Н | А | |
| R | Ом | |
| ωН | рад/с | |
| U | В | |
| L | 0.1 | Гн |
| J | 0.25 | кг·м2 |
В ячейке A1 рассчитаем коэффициент c (рис. 3.51).

Рис. 3.51
В ячейке B1 рассчитаем шаг интегрирования (рис. 3.52).

Рис. 3.52
В столбце A, начиная с ячейки A3, будет размещён массив време-
ни. В столбце
B, начиная с ячейки B3, будет размещён массив тока. В
столбце C, начиная с ячейки C3, будет размещён массив скорости. В массив A3-C3 внесем нули, так как переходный процесс рассчитывается с нулевыми начальными условиями (рис. 3.53).
Рис. 3.53
Выделим ячейку B1, скопируем содержимое ячейки в буфер с по- мощью сочетания клавиш <Ctrl> + <C>. Вставим содержимое буфера в ячейку A4 с помощью сочетания клавиш <Ctrl> + <V>. В правом ниж- нем углу выберем раскрывающийся маркированный список и в нём от- метим пункт «Значения и форматы чисел». Аналогично внесём скопи- рованную информацию из B1 в E3. Содержимое ячейки E3 удвоим (рис.
3. 54).

Рис. 3.54
Удвоенное значение шага интегрирования внесём в ячейку А5, выделив в параметрах вставки пункт «Значения и форматы чисел». Вы- делим ячейки A4-A5 и продолжим выделение до ячейки A250.
В ячейку B4 внесём формулу для второй итерации расчёта тока
(рис. 3.55).

Рис. 3.55
В ячейку C4 внесём формулу для второй итерации расчёта скоро-
сти (рис. 3.56).

Рис. 3.56
Выделим массив ячеек A4-C4 и продолжим выделение до A250- C250. Получен числовой массив решения системы дифференциальных уравнений. Выделим массив A3-C250. Вызовем «мастер диаграмм», по аналогии с предыдущими диаграммами построим графики переходных процессов тока и скорости (рис. 3.57).
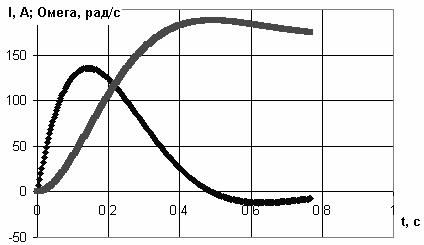
Рис. 3.57
Определим величину броска тока. Для этого в ячейку F3 вставим функцию МАКС из категории «Статистические». В меню функции вве- дём диапазон значений тока: B3-B250.
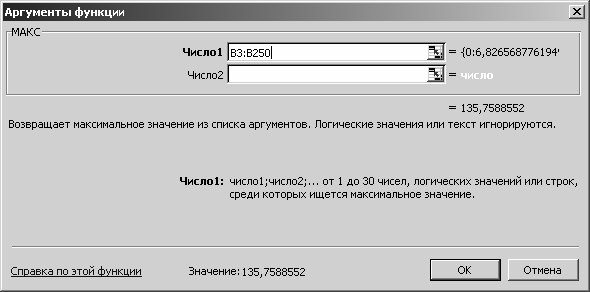
Рис. 3.58
В ячейке F3 получим величину броска тока якоря: 135,7589 А
(рис. 3.59).

Рис. 3.59
Определим максимум противотока или минимум тока и запишем его в ячейке G3. Для этого воспользуемся функцией МИН из категории
«Статистические». В меню функции выделяем диапазон B3-B250 (рис.
3.60).
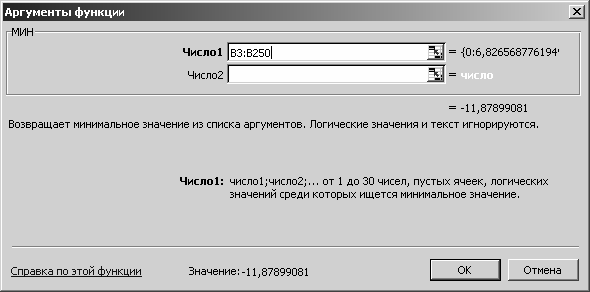
Рис. 3.60
Величина противотока составит -11.879 А (рис. 3.61).
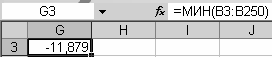
Рис. 3.61
Определим перерегулирование по скорости как
∆ω%= ωМ
−ωУ
⋅100%, .
где ωМ
ωУ
ωУ
– максимальная скорость во время переходного процесса,
– установившаяся скорость.
(3.48)
Установившаяся скорость в данной задаче равна номинальной
ωУ = 157 рад/с .
Для определения максимальной скорости в ячейку H3 введём
функцию МАКС с диапазоном C3-C250 (рис. 3. 62).

Рис. 3.62
В ячейке I3 согласно (3.48) рассчитаем, что перерегулирование по скорости при пуске ДПТ с НВ составит 19.626% (рис. 3.63).

Рис. 3.63
Итак в данной главе средствами Excel рассчитан переходный про- цесс пуска ДПТ с НВ, определено, что бросок тока и противоток соста- вят соответственно 135,7589 А и -11.879 А, перерегулирование составит
19.626%.
ГЛАВА 6.
ПОСТРОЕНИЕ ХАРАКТЕРИСТИК В ПРОГРАММЕ EXCEL, ЗА-
Дата добавления: 2016-04-02; просмотров: 1251;
