Расчёт цепи постоянного тока методом Крамера

Откроем новый лист Excel. Разместим матрицу коэффициентов в массиве A1-C3, матрицу свободных членов в массиве E1-E3 (рис. 3.13). Для определения токов в цепи методом Крамера найдём определитель матрицы A. Разместим его в ячейку A5. Вызовем мастер функций и в категории «Математические» выберем функцию «МОПРЕД» (рис. 3.20).

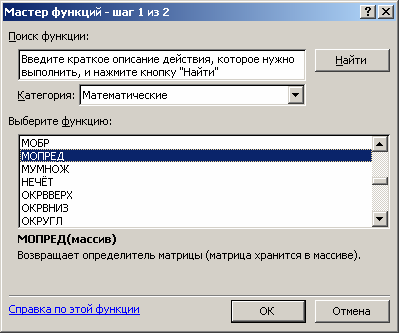
Рис. 3.20

В меню «Аргументы функции» введём адрес массива коэффици-

ентов A1-C3 (рис. 3.21).

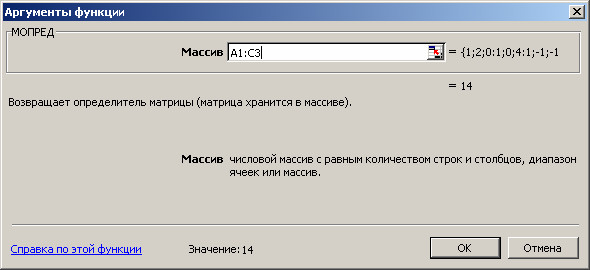
Рис. 3.21

Полный определитель размещён в ячейке A5 и равен 14 (рис. 3.22).

Рис. 3.22

Скопируем массив ячеек A1-C3 в G1-I3, заполним массив G1-G3 содержимым массива E1-E3. Получится первая замещённая матрица ко- эффициентов. Скопируем массив ячеек A1-C3 в J1-L3, заполним массив K1-K3 содержимым массива E1-E3. Получится вторая замещённая мат- рица коэффициентов. Скопируем массив ячеек A1-C3 в M1-O3, запол- ним массив O1-O3 содержимым массива E1-E3. Получится третья за- мещённая матрица коэффициентов (рис. 3.23).

Рис. 3.23

Найдём первый частный определитель от матрицы, размещённой в массиве ячеек G1-I3, разместим его в ячейку A7. Найдём второй част- ный определитель от матрицы, размещённой в массиве ячеек J1-L3, разместим его в ячейку B7. Найдём третий частный определитель от матрицы, размещённой в массиве ячеек M1-O3, разместим его в ячейку C7. Ток I1 получим, поделив содержимое ячейки A7 на A5. Результат разместим в ячейке A8. Ток I2 получим, поделив содержимое ячейки B7

на A5. Результат разместим в ячейке

B8. Ток I3 получим, поделив со-

держимое ячейки C7 на A5. Результат разместим в ячейке C8 (рис. 3.24).

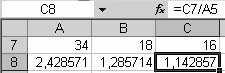
Рис. 3.24

Как и следовало ожидать результаты расчётов с использованием методов Крамера и обратной матрицы совпадают.

§3.3. Расчёт цепи переменного тока, определение фазы потребляе-