Расчёт цепи постоянного тока методом обратной матрицы
Пусть дана электрическая цепь (рис. 3.12), состоящая из трёх вет-
вей. Известны величины ЭДС источников:
E1 = 10 В ,
E2 = 5 В ,
E3 = 3 В
и сопротивлений в каждой ветви:
R1 =1 Ом ,
R2 = 2 Ом ,
R3 = 4 Ом .
Необходимо определить токи, протекающие в каждой ветви.
R1
I1 I2
R2
R3
| I |
E1 E2 E3
Рис. 3.12. Цепь постоянного тока
Для трёх неизвестных токов I1, I2, I3 составим систему из трёх уравнений согласно первому и второму законам Кирхгофа
⎧E = I ⋅R + I ⋅R + E
⎪ 1 1 1 2 2 2
= ⋅ + ⋅ + (3.18)
⎨E1
I1 R1
I3 R3 E3
| ⎩ |
и преобразуем её следующим образом
⎧I1 ⋅R1 + I2 ⋅R2 + I3 ⋅0 = E1 − E2
⎪I ⋅R + I
⋅0 + I ⋅R
= E− E
. (3.19)
⎨ 1 1 2 3 3 1 3
| ⎩ |
Подставим в (3.19) численные данные и получим матрицу коэф-
фициентов
⎡R1 R2
0 ⎤ ⎡1 2 0 ⎤
A= ⎢R
0 R⎥ = ⎢1 0 4 ⎥
(3.20)
⎢ 1 3 ⎥ ⎢ ⎥
⎢⎣ 1 −1
и матрицу свободных членов
−1⎥⎦
⎢⎣1
−1 −1⎥⎦
⎡E1 − E2 ⎤
⎡10 − 5⎤ ⎡5⎤
| ⎢ 1 3 ⎥ ⎢ ⎥ ⎢ ⎥ . |
⎣⎢ 0
⎦⎥ ⎢⎣ 0 ⎥⎦
⎢⎣0⎥⎦
Решение системы уравнений (3.18) найдём как
⎡I1 ⎤
| ⎢ |
⎥ = A−1 B .
(3.22)
| 2 ⎥ |
Матрицу коэффициентов (3.20) внесём в массив A1-C3, а матрицу свободных членов (3.21) внесём в массив E1-E3 (рис. 3.13).
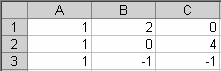
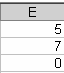 Рис. 3.13
Рис. 3.13
Обратную матрицу от матрицы коэффициентов разместим в мас- сиве G1-I3. Вызовем мастер функций и в категории «Математические» выберем «МОБР» (рис. 3.14).
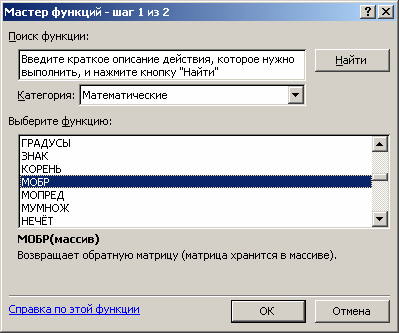
Рис. 3.14
В окне «Аргументы функции» введём адрес источника данных
A1:C3 (рис. 3.15).
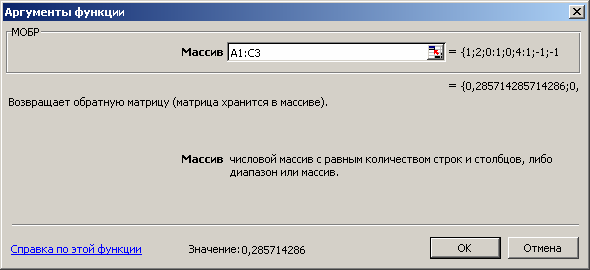
Рис. 3.15
В справке программы Excel по этой функции сказано, что форму- лу необходимо ввести как формулу массива. Нажмите клавишу F2, а за- тем нажмите клавиши <CTRL>+<SHIFT>+<ENTER>. Если формула не будет введена как формула массива, единственное значение будет равно
0,285714. В результате получим обратную матрицу (рис. 3.16).
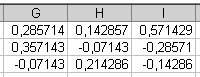
Рис. 3.16
Умножим обратную матрицу,
размещённую в ячейках G1-I3, на
матрицу свободных членов, размещённую в ячейках E1-E3. Для этого выделим массив ячеек результата F14-F16, вызовем с помощью мастера функций функцию «МУМНОЖ» из категории «Математические» (рис.
3.17).
рис. 3.17
В опции «Аргументы массива» введём адрес первого массива G1- I3 и адрес второго массива E1-E3 (рис. 3.18). Нажмите клавишу F2, а за- тем нажмите клавиши <CTRL>+<SHIFT>+<ENTER>.
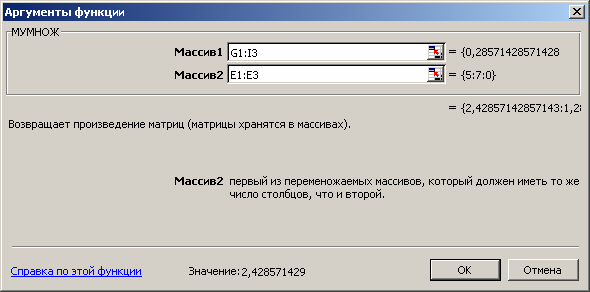
Рис. 3.18
Полученный результат (рис. 3.19)
⎡I1 ⎤
⎡2,428571⎤
| I |
| 2 ⎥ ⎢ ⎥ , |
| ⎢ |
(3.23)
⎢⎣I3 ⎥⎦
⎢⎣1,142857⎥⎦
размещённый в ячейках F14-F15, является истинным, так как выполня-
ется первый закон Кирхгофа – третье уравнение системы (3.18).
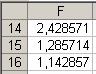
Рис. 3.19
Проверку полученного результата можно выполнить и по первому и второму уравнениям системы (3.18).
Дата добавления: 2016-04-02; просмотров: 799;
