Расчёт надёжности системы с параллельным соединением элементов

Отказ системы произойдёт при отказе всех элементов (рис. 5.5).

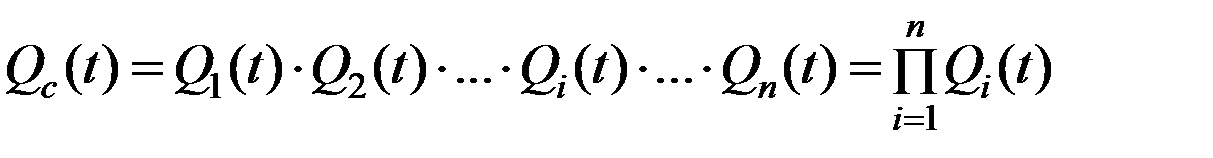, (5.8)

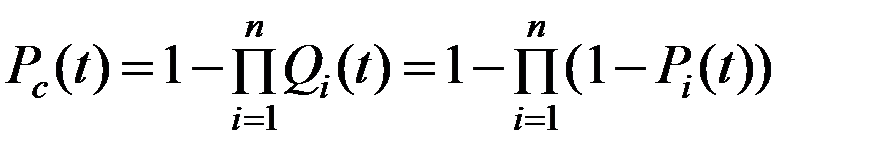. (5.9)

Например, при P_i(t) = 0,86, n = 3 получают .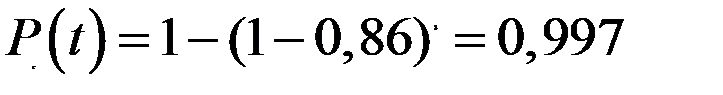

Рис. 5.5. Расчетная схема параллельного соединения элементов

При параллельном соединении можно сформировать надёжную конструкцию из самых ненадёжных элементов:

(P(t) + Q(t))^m = 1,

где m – количество элементов.

Например, при m = 2: (P(t) + Q(t))^m = P² + 2PQ + Q² = 1,

здесь P² означает вероятность безотказной работы обоих элементов;

2PQ – вероятность отказа одного элемента, при этом второй элемент останется работоспособным;

P² + 2PQ – из строя выйдет (откажет) не более одного элемента;

Q² – вероятность отказа обоих элементов;

P = Q = 0,5; 0,25 + 0,5 + 0,25 = 1;

при m = 3: (P(t) + Q(t))^m =Р³ + 3Р²Q + 3РQ² + Q³ = 1,

Р³ – все три элемента работоспособны;

3Р² Q – из строя выйдет не более одного элемента;

3QP² – из строя выйдет не более двух элементов;

Q³ – из строя выйдут все три элемента.

Из приведенного примера видно, что надёжность системы с параллельным соединением повышается при увеличении числа элементов.

При экспоненциальном распределении наработки выражение (5.9) принимает вид:

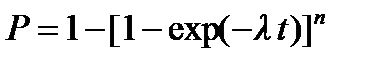, (5.10)

откуда после интегрирования и преобразований средняя наработка системы определяется:

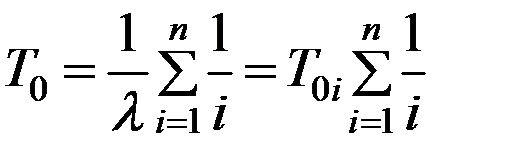, (5.11)

где 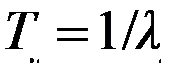− средняя наработка элемента.

При больших значениях n справедлива приближенная формула

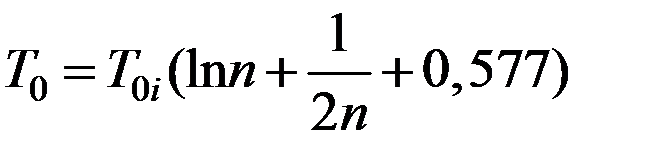. (5.12)

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки её элементов (например, при 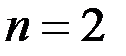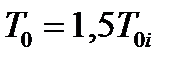, при n = 3 ).

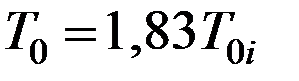Контрольные вопросы

1. Что такое система с последовательным соединением элементов, каковы условия её безотказной работы?

2. Что такое система с параллельным соединением элементов, каковы условия ее безотказной работы?

3. Как рассчитывается вероятность безотказной работы систем с параллельным соединением элементов?

4. Как можно повысить надёжность систем с параллельным соединением элементов?

5. Как определяются такие показатели безотказности системы с параллельным соединением элементов, как вероятность безотказной работы и средняя наработка системы?