Анализ сложных систем

Проблема эффективности технических систем является одной из основных. Она непосредственно связана с проблемами надёжности и экономичности.

Возрастание сложности технических систем приводит к снижению их надежности, следовательно, к уменьшению их эффективности.

Недостаточная надежность проектируемой или существующей технической системы может стать проблемой, для решения которой нужно выдвинуть альтернативные цели (например, отказ от производства системы или замена ее новой, более совершенной установкой; повышение надёжности существующей системы до требуемого уровня; улучшение условий эксплуатации существующей системы и т. д.).

На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. В качестве примера показана система, изображённая на рис. 5.6.

Рис. 5.6. Система со сложным соединением элементов

Примерами систем со сложным соединением элементов могут быть дорожная сеть, соединение энергетических систем и др.

В системе, изображённой на рис. 5.6, отказ элемента А нарушает сразу два пути АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остаётся работоспособной.

Для определения вероятности безотказной работы системы или надёжности функционирования системы используют несколько методов. Рассмотрим самый простой – метод прямого перебора. С помощью этого метода можно определить надёжность работы любого типа технических систем, он легко поддаётся проверке, и, главное, он позволяет рассмотреть влияние отказов элементов на работу системы, т. е. на устойчивость функционирования системы. Недостатком данного метода является громоздкость и трудность в составлении универсальной программы для применения вычислительной техники.

Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д.

При рассмотрении системы, изображённой на рис. 5.6, предполагается, что в данном случае элементы системы имеют следующие вероятности безотказной работы:

Р(А) = 0,9; Р(В) = 0,8; Р(С) = 0,6; Р(Д) = 0,7.

Событие А определяется как событие, состоящее в том, что элемент А работает безотказно, тогда Ā – событие, состоящее в том, что элемент А отказал. Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты всех вычислений записываются в табл. 5.1.

Таблица 5.1

Таблица состояний

№ состояния	Число отказавших элементов	События, характеризующие состояние системы	Вероятность состояния системы	Отметка о работоспособности системы, изображённой на рис. 5.6
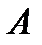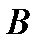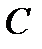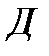
		∩ ∩ ∩	0,3024	+
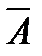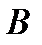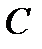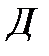
		∩ ∩ ∩	0,0336	+
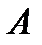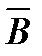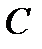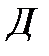
		∩ ∩ ∩	0,0756	+
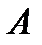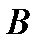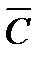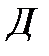
		∩ ∩ ∩	0,1295	+
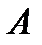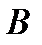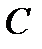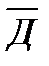
		∩ ∩ ∩	0,2016	+
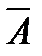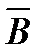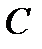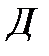
		∩ ∩ ∩	0,0084	–

Окончание табл. 5.1

№ состояния	Число отказавших элементов	События, характеризующие состояние системы	Вероятность состояния системы	Отметка о работоспособности системы, изображённой на рис. 5.6
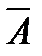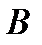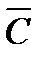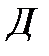
		∩ ∩ ∩	0,0144	+
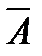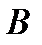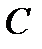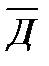
		∩ ∩ ∩	0,0224	–
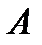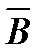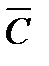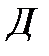
		∩ ∩ ∩	0,0324	+
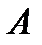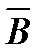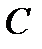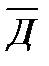
		∩ ∩ ∩	0,0504	+
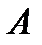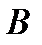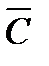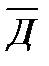
		∩ ∩ ∩	0,0864	–
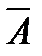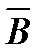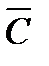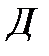
		∩ ∩ ∩	0,0036	–
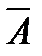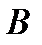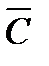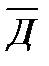
		∩ ∩ ∩	0,0096	–
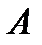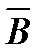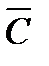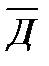
		∩ ∩ ∩	0,0056	–
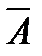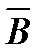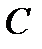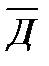
		∩ ∩ ∩	0,0216	–
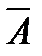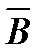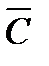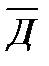
		∩ ∩ ∩	0,0024	–
		∑	1,0000	0,8400

Первая строка табл. 5.1 заполняется следующим образом: вначале предполагается, что в системе не отказал ни один элемент, А ∩ В ∩ С ∩ Д, вероятность этого вычисляется по формуле

Р⁽⁰⁾ = Р(А)Р(В)Р(С)Р(Д) = 0,9 × 0,8 × 0,6 × 0,7 = 0,3024.

В графе «Отметка о работоспособности» ставится знак «+», если система работоспособна, и знак «–», если неработоспособна.

Вторая строка табл. 5.1 предполагает, что в системе отказал один элемент (элемент А), Ā ∩ В ∩ С ∩ Д, вероятность такого состояния системы:

Р⁽¹⁾ = Р(Ā)Р(В)Р(С)Р(Д) = 0,1 × 0,8 × 0,7 × 0,6 = 0,0336 при Р(А) = 1 – Р(Ā),

где Р(Ā) и Р(А) – вероятности отказа и безотказной работы элемента А.

Остальные строки табл. 5.1 заполняются аналогично с учетом отказа одного, двух, трёх и четырёх элементов системы.

Таким образом, система со сложным соединением элементов (подсистем) имеет вероятность безотказной работы 0,84.

Оценивая устойчивость функционирования технической системы, необходимо знать ее поведение в будущем. Если бы системы и объекты были безотказны, то большинство проблем, связанных с безопасностью, исчезло бы.
Но все объекты, изделия и системы невечны, поэтому необходимо знать срок их безотказной работы, чтобы исключить аварии, вызванные отказами.

Контрольные вопросы

1. Приведите пример системы со сложным соединением элементов.

2. С помощью какого метода анализируются системы со сложным соединением элементов?

3. Назовите преимущества и недостатки метода прямого перебора.