Расчёт надёжности систем с последовательным соединением элементов

Работоспособность системы с последовательным соединением элементов обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии (рис. 5.4).

X Y

P₁( t) P₂(t) P_i(t) P_n(t)

Рис. 5.4. Расчётная схема последовательного соединения элементов

Безотказность работы i-го элемента зависит от безотказности других:

Р_с(t) = Р₁(t) · Р₂(t) · … · Р_i(t) · … · Р_n(t) = 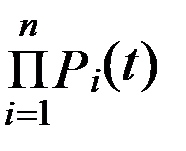; (5.1)

Q_с(t) = 1 – Р_с(t) = 1– 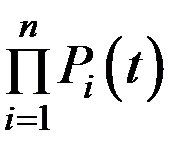; (5.2)

;

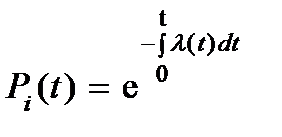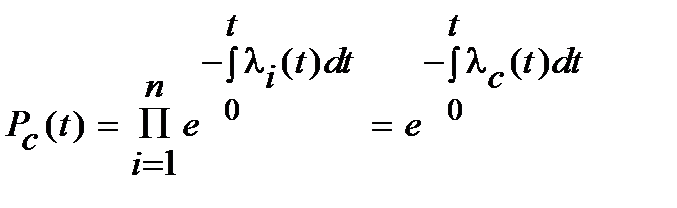; (5.3)

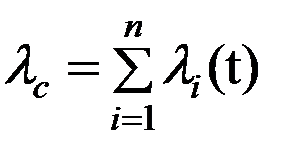; (5.4)

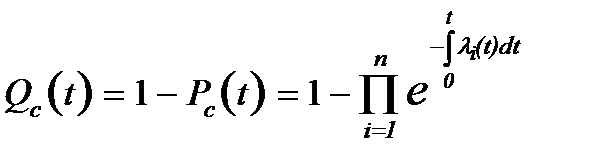. (5.5)

Если все элементы одинаковы, то:

1) при n = 30 Р₁ = Р₂ = … = Р_i = … Р_n;

Р_с(t) = Р(t)ⁿ;

Р(t) = 0,99;

Р_с(t) = 0,99³⁰ = 0,7397;

2) при n = 500

Р_с(t) = 0,0066.

Из (5.3)–(5.4) следует, что для системы из n элементовc одинаковой надежностью (λ = λ₁) верно условие:

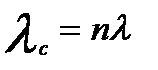; (5.6)

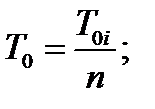(5.7)

т. е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.При последовательном соединении общая надёжность всей системы ниже надёжности самого слабого элемента. При очень большом количестве высоконадёжных элементов система может оказаться неработоспособной.

Повысить надёжность такой системы можно за счёт выполнения следующих действий:

– увеличения надёжности составных элементов;

– сокращения количества элементов;

– уменьшения интенсивности отказов (за счет уменьшения времени эксплуатации).

Контрольные вопросы и задачи

1. Что такое последовательная система и в чем состоит условие её безотказной работы?

2. Как рассчитывается вероятность безотказной работы систем с последовательным соединением элементов?

3. Как можно повысить надёжность систем с последовательным соединением элементов?

4. Как определяются такие показатели безотказности системы с последовательным соединением элементов, как вероятность безотказной работы и интенсивность отказов?

5. Какой закон распределения наработки до отказа будет иметь система с последовательным соединением элементов, если законы распределения наработки до отказа элементов являются экспоненциальными?

6. Структура проектируемой системы представляется системой с последовательным соединением элементов, состоящей из 10 элементов A, 15 элементов B, 32 элементов D и 8элементов F. Интенсивности отказов элементов известны и равны:

λ_A = 2 · 10^–6 ч^–1 , λ_B = 4 · 10^–6 ч^–1, λ_D = 2,5 · 10^–6 ч ^–1, λ_F = 5 · 10^–6 ч^–1.

Определить среднюю наработку до отказа T_0с и ВБР системы при наработках

t₁ = 100 ч, t₂= 1000 ч.

Ответ: T_0с = 5 · 10³ ч, P(t₁) = 0,98, P(t₂) = 0,819.