Типовые логические структуры надёжности
| Равнонадежные элементы |
| Элементы различной надежности |
| Графы состоний |
| Структурная логическая схема |

Обозначения на графах состояний:
1 – работоспособное состояние элемента,
0 – неработоспособное состояние элемента.
Контрольные вопросы
1. В чём особенности марковского случайного процесса, на основе которого строится расчётная модель для восстанавливаемых объектов и систем?
2. Назовите основные этапы составления расчётной модели.
3. Поясните мнемоническое правило составления дифференциального уравнения вероятностей состояния (уравнение Колмогорова – Чепмена).
4. Дайте определение и поясните смысл показателей надежности восстанавливаемых объектов и систем.
5. Каковы особенности применения метода дифференциальных уравнений для расчета надежности невосстанавливаемых объектов?
6. На любом из примеров поясните связь графа состояний с логической структурой надёжности.
4.6. Пример расчёта безотказности
с использованием модели «прочность – нагрузка»
1. Рассчитать элемент, на который действует растягивающая нагрузка (рис. 4.18).
Принимается, что растягивающая нагрузка Р и предел прочности на
растяжение s являются случайными величинами, подчиняющимися нормальному закону распределения вероятностей с параметрами соответственно:
Р = 17 800 Н, 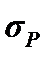 = 445 МПа и s = 690 МПа,
= 445 МПа и s = 690 МПа, 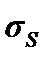 = 34,5 МПа. Заданное значение безотказности R3 = 0,9999.
= 34,5 МПа. Заданное значение безотказности R3 = 0,9999.

Рис. 4.18. Элемент, на который действует растягивающая нагрузка
Решение: растягивающее напряжение определяется по формуле 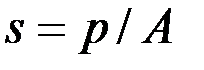 , где
, где  . Допуск на радиус выражается в виде доли
. Допуск на радиус выражается в виде доли 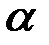 от номинального значения r:
от номинального значения r: 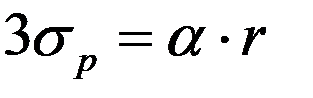 ,
, 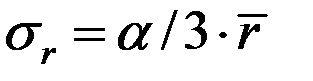 .
.
По формулам расчета математического ожидания и среднеквадратического отклонения линейной функции случайной величины получается:  =
=  ;
;

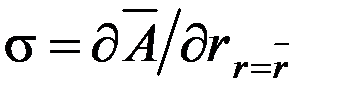 ;
;  ;
; 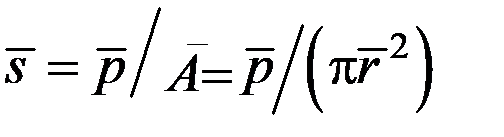 ;
;
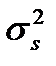 =
= 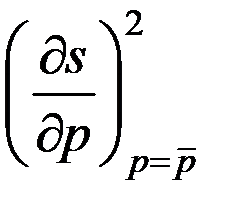 ·
·  р+
р+ 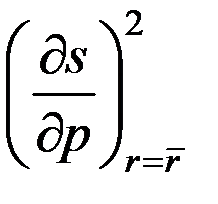 ·
·  r =
r =
= 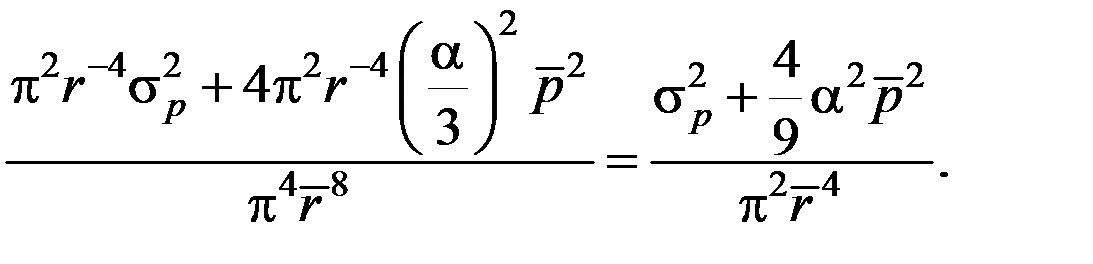
Плотность распределения прочности:
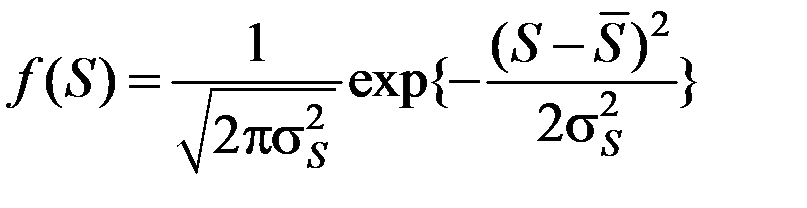 .
.
Плотность распределения нагрузки:
 .
.
Плотность распределения разности S – s, соответственно, имеет вид:
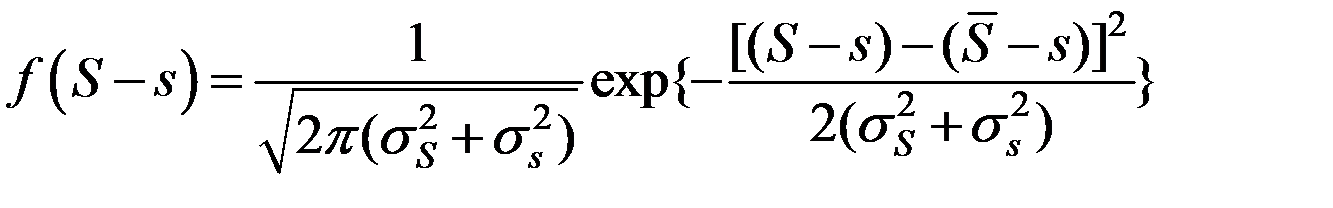 .
.
Условие параметрической безотказности определяется равенством:
R = P{S – s > 0}.
Статистический запас прочности находится из выражения для Р(S – s):
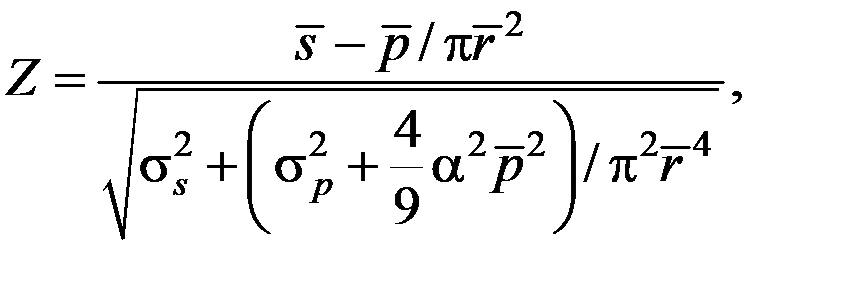
где Z − квантиль стандартного нормального распределения.
Для R3 = 0,9999 по таблицам стандартного нормального распределения находится Z = 3,72. При 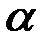 = 0,015 выполняется равенство
= 0,015 выполняется равенство
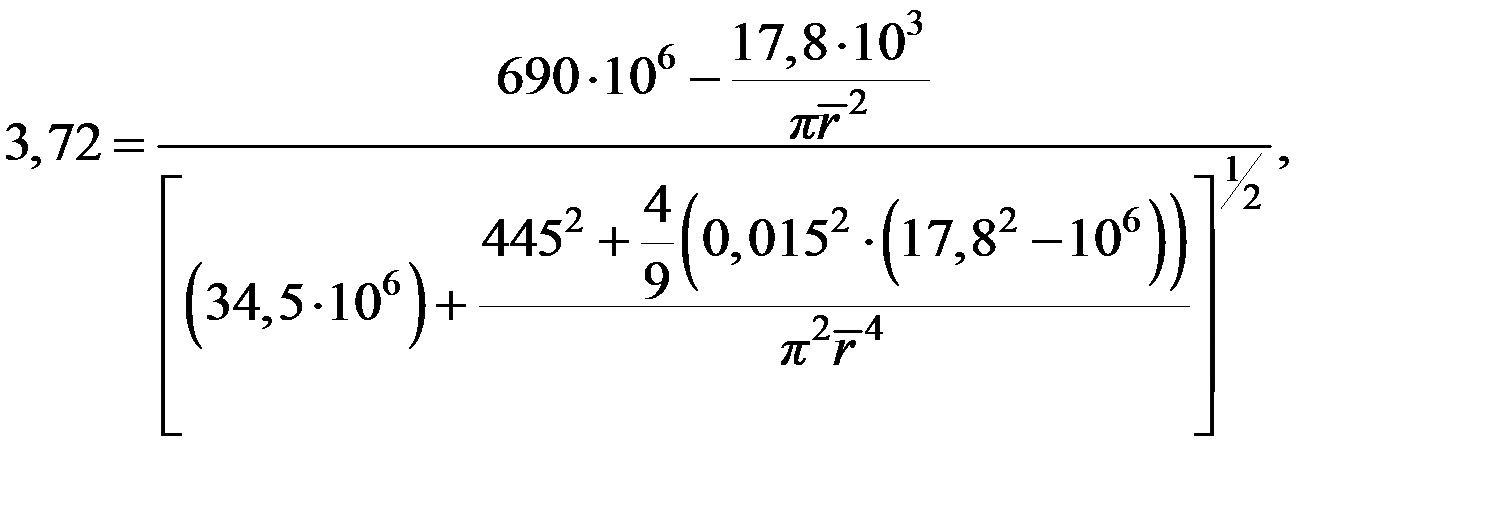
откуда 144,6 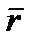 4 – 24,6
4 – 24,6 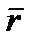 2 + 1 = 0 и окончательно для положительных корней уравнения
2 + 1 = 0 и окончательно для положительных корней уравнения 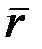 1 = 2,60 мм;
1 = 2,60 мм; 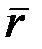 = 3,21 мм, соответственно R = 0,0001; R = 0,9999.
= 3,21 мм, соответственно R = 0,0001; R = 0,9999.
Влияние допуска 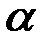 и изменчивости прочности материала на надежность элемента представлено в табл. 4.5 и 4.6.
и изменчивости прочности материала на надежность элемента представлено в табл. 4.5 и 4.6.
Таблица 4.5
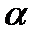 , % , %
| 1,5 | 1,5 | ||
| Z | 3,72 | 3,61 | 3,36 | 3,1 |
| R | 0,9999 | 0,9998 | 0,9996 | 0,999 |
Дата добавления: 2016-02-16; просмотров: 886;
