Вынужденные колебания

Колебания, возникающие под действием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями.

;

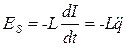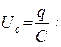
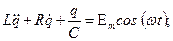
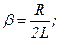
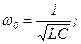
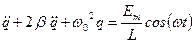
дифференциальное неоднородное уравнение 2-го порядка относительно q.

Решение этого уравнения: q = q_mCos(ωt – ψ),

где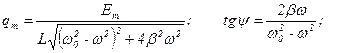

В эти формулы подставляем значения β и ω₀:

; .

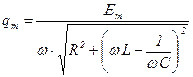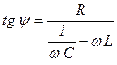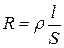– омическое или активное сопротивление – сопротивление проводников, одинаковое как для постоянного, так и для переменного тока. Величина R определяется свойствами проводника.

Кроме активных сопротивлений R, в цепях переменного тока имеются реактивные сопротивления: X_L и X_C. Они отличаются от активных сопротивлений тем, что не преобразуют электрическую энергию в тепловую.

Геометрическая сумма активных и реактивных сопротивлений называется полным сопротивлением Z (импедансом).

X_L =ωL – реактивное индуктивное сопротивление (или просто индуктивное);

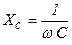– реактивное емкостное сопротивление (или просто емкостное).

С и L – реактивные элементы. X = X_L – X_C – реактивное сопротивление.

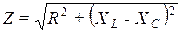– импеданс.

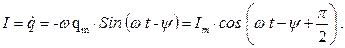
Обозначим φ = ψ – π/2, тогда I = I_m cos (ωt – φ),

где амплитуда тока 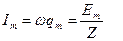– закон Ома.

Таким образом, φ – сдвиг по фазе между током I и приложенной ЭДС E = E_m cos(ωt), т.е. ток отстает от ЭДС на угол φ.

По 2-му правилу Кирхгофа: U_R + U_C + U_L = E_m cos(ωt), где

;

; .

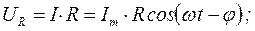
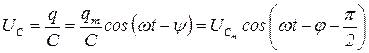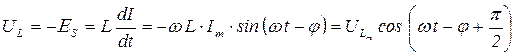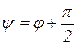Таким образом, эти формулы показывают, что напряжение на конденсаторе U_C отстает по фазе от тока на угол π/2, а напряжение на катушке U_L опережает ток на π/2. Напряжение на активном сопротивлении U_R изменяется в фазе с током.

На рисунке приведена векторная диаграмма последовательного соединения элементов.

Установившиеся вынужденные колебания – это и есть переменный ток.

Резонанс

Резонанс – резкое возрастание амплитуды вынужденных колебаний осциллятора: А =max. Это возможно, когда ω ≈ω₀.

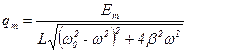
Знаменатель должен быть минимальным:

(ω₀² – ω²)² + 4 β² ω² = min,

т.е. производная должна быть равна 0. Взяв производную по ω, получаем: .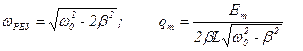

Если β = 0 (нет R), то ω_рез = ω₀ и q_m = ∞. Когда ω = 0, то q_m = E_m • С

На рисунках представлены резонансные кривые для q_m и I_m. Резонансные кривые для U_Cm такие же как и для q_m.

.

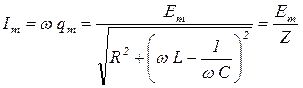Когда ω = 0, то I_m = 0;

I_m = max, если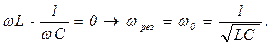

.

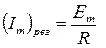
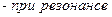Форма резонансных кривых связана с добротностью контура Q. Добротность контура связана с шириной резонансной кривой: 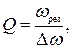Δω – ширина резонансной кривой. Δω находится на «высоте», равной 0,7 от максимальной, т.е. в резонансе.

Следовательно, острота резонансной кривой связана с добротностью контура.

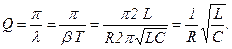
Из векторной диаграммы: ,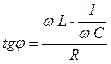

φ – сдвиг по фазе между током I и E.

При резонансе I_m = max и 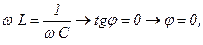т.е.сила тока I и приложенное напряжение E изменяются синфазно. Тогда Z = min → Z = R →

U_R = E = U, т.е. внешнему напряжению, и U_mC = U_mL, но противоположны по фазе.

Такой резонанс (последовательный резонанс) называется резонансом напряжений.

.

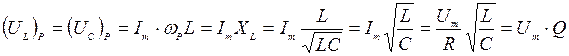Так как. Q > 1,то U_L > U и U_С > U, поэтому резонанс напряжений используется в технике для усиления колебаний напряжения какой-либо определенной частоты.

Резонанс напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, т.к. иначе может наблюдаться пробой.