Методика и техника эксперимента. Колебательным контуром называется цепь, состоящая из конденсатора С, катушки индуктивности L и омического сопротивления R
 Колебательным контуром называется цепь, состоящая из конденсатора С, катушки индуктивности L и омического сопротивления R. Если зарядить конденсатор до разности потенциалов U, а затем дать ему возможность разряжаться через индуктивность L, то в колебательном контуре возникают свободные колебания тока, заряда на обкладках конденсатора и напряжения между обкладками конденсатора. В процессе колебаний, энергия электрического поля заряженного конденсатора преобразуется в энергию магнитного поля катушки индуктивности и, наоборот, энергия магнитного поля преобразуется в электрическую энергию. При протекании тока в контуре в активном сопротивлении выделяется джоулево тепло, что приводит к потере энергии и затуханию колебаний. В связи с этим, с течением времени амплитуда колебаний уменьшается так, как показано на рисунке.
Колебательным контуром называется цепь, состоящая из конденсатора С, катушки индуктивности L и омического сопротивления R. Если зарядить конденсатор до разности потенциалов U, а затем дать ему возможность разряжаться через индуктивность L, то в колебательном контуре возникают свободные колебания тока, заряда на обкладках конденсатора и напряжения между обкладками конденсатора. В процессе колебаний, энергия электрического поля заряженного конденсатора преобразуется в энергию магнитного поля катушки индуктивности и, наоборот, энергия магнитного поля преобразуется в электрическую энергию. При протекании тока в контуре в активном сопротивлении выделяется джоулево тепло, что приводит к потере энергии и затуханию колебаний. В связи с этим, с течением времени амплитуда колебаний уменьшается так, как показано на рисунке.

|
Выведем уравнение затухающих колебаний. Полагая, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока, применим к колебательному контуру второе правило Кирхгофа:
I·R + UС = ES, (6.5)
где IR – падение напряжения на резисторе; UС = 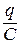 – напряжение на конденсаторе; ES= – L
– напряжение на конденсаторе; ES= – L  – ЭДС самоиндукции.
– ЭДС самоиндукции.
Так как I =  , а q = C·U, тогда I = C
, а q = C·U, тогда I = C  . Найдем производную силы тока:
. Найдем производную силы тока:  . Подставляя эти выражения в уравнение (6.5), получим:
. Подставляя эти выражения в уравнение (6.5), получим:
 +
+ 
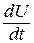 +
+ 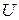 = 0. (6.6)
= 0. (6.6)
Разделив уравнение (6.6) на LC получим:
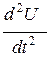 +
+ 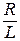
 +
+ 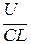 = 0. (6.7)
= 0. (6.7)
Выражение (6.7) представляет собой дифференциальное уравнение затухающих колебаний, возникающих в колебательном контуре.
Решением этого уравнения является функция:
 (6.8)
(6.8)
где β = R/2L – коэффициент затухания.
Так как циклическая частота собственных колебаний контура равна ω02 = 1/LC, то уравнение (6.7) можно представить в виде:
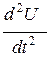 + 2β
+ 2β  + ω02U = 0. (6.9)
+ ω02U = 0. (6.9)
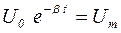 – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;
ω = 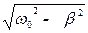 – частота затухающих колебаний; φ – начальная фаза.
– частота затухающих колебаний; φ – начальная фаза.
Из выражения для частоты ω следует, что затухающие колебания в контуре возникают лишь в том случае, если:
ω02 >β2; 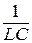 >
>  ; R < 2
; R < 2  .
.
Если R >  , то колебания в контуре не возникают, а происходит, так называемый апериодический разряд конденсатора.
, то колебания в контуре не возникают, а происходит, так называемый апериодический разряд конденсатора.
Для характеристики степени затухания колебаний, кроме коэффициента затухания β, используют также логарифмический декремент затухания.
Логарифмическим декрементом затухания λ называется натуральный логарифм отношения двух амплитуд напряжения Um, разделенных интервалом времени, равным периоду колебаний Т:
λ = ln  , (6.10),
, (6.10),
где Um1 = U0 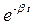 ; Um2 = U0
; Um2 = U0  .
.
Подставив значения Um в формулу (6.8), получим:
λ = β·T. (6.11)
Принципиальная схема для получения затухающих колебаний представлена ниже:

Она представляет собой колебательный контур, состоящий из конденсатора С, катушки индуктивности L и сопротивления R. Колебания в контуре наблюдаются с помощью осциллографа ОЭ. Для возбуждения колебаний служит звуковой генератор ГЗ-111.
Дата добавления: 2016-02-16; просмотров: 908;
