Колебательный контур
В электрической цепи, состоящей из последовательно соединенных конденсатора С, катушки индуктивности L и омического сопротивления R (рис. 6.1), могут возникать электромагнитные колебания. Поэтому такую цепь называют колебательным контуром.
 Ток, текущий в колебательном контуре, является переменным i = f (t). Закон Ома и вытекающие из него правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми для мгновенных значений переменного тока и напряжения, если только их изменения происходят не слишком быстро.
Ток, текущий в колебательном контуре, является переменным i = f (t). Закон Ома и вытекающие из него правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми для мгновенных значений переменного тока и напряжения, если только их изменения происходят не слишком быстро.
Если мгновенные значения I и U во всех сечениях цепи будут практически одинаковыми, то такие токи называются квазистационарными.
Рассмотрим колебания, происходящие в идеализированном контуре, сопротивление которого пренебрежимо мало (R ≈ 0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±q. При этом вся энергия колебательного контура сосредоточена в конденсаторе и равна 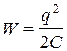 . Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки
. Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки 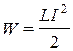 . Когда конденсатор полностью разрядится, ток в цепи достигнет максимума. С этого момента ток, не меняя направление, начнет убывать, но из-за ЭДС самоиндукции он прекратится не сразу.
. Когда конденсатор полностью разрядится, ток в цепи достигнет максимума. С этого момента ток, не меняя направление, начнет убывать, но из-за ЭДС самоиндукции он прекратится не сразу.
В колебательном контуре (Рис. 6.1) будут происходить свободные электромагнитные колебания.
Рассмотрим идеальный случай: R = 0.
1 стадия: В начальный момент времени t = 0 зарядим конденсатор.
2 стадия: Замкнув конденсатор на катушку, конденсатор начнет разряжаться и в контуре потечет ток. Из-за явления самоиндукции ток в контуре постепенно увеличивается и сила тока I достигнет максимума в момент времени t = Т/4, когда заряд на конденсаторе станет равным нулю q = 0. Энергия электрического поля будет уменьшаться, но зато возникает всё возрастающая энергия магнитного поля. Т.к. R = 0, энергия не расходуется на нагревание проводов и полная энергия сохраняется:








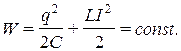

 t = 0 t = Т/4 t = Т/2 t = ¾Т t = Т
t = 0 t = Т/4 t = Т/2 t = ¾Т t = Т
U = max U = 0 U = max U = 0 U = max
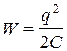
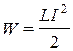

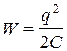
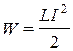
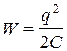 I = 0 I = max I = 0 I = max I = 0
I = 0 I = max I = 0 I = max I = 0
3 стадия: Далее ток I уменьшается из-за явления самоиндукции, и когда U = max, I = 0.
4 и 5 стадии: Затем те же процессы протекают в обратном направлении, после чего система приходит в первоначальное состояние.
Таким образом, периодически изменяются q, U, I. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.
Найдем уравнение колебаний идеального колебательного контура:
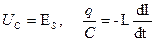 .
.
Учитывая, что 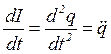 получим
получим 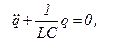 где
где 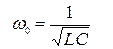 -собственная частота:
-собственная частота:
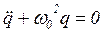 (6.1)
(6.1)
– дифференциальное уравнение собственных колебаний (R = 0).
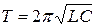 - формула Томсона.
- формула Томсона.
Решение уравнения (6.1):
q = qmSin (ω0 t + α). (6.2)
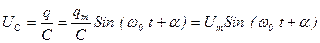 (6.3)
(6.3)
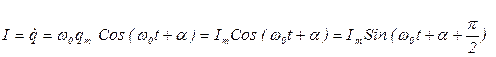 . (6.4)
. (6.4)
 Таким образом, ток опережает по фазе напряжение на конденсаторе на π/2.
Таким образом, ток опережает по фазе напряжение на конденсаторе на π/2.
Дата добавления: 2016-02-16; просмотров: 776;
