Соотношения между фазными и линейными напряжениями источников

Фазные напряжения источника отличаются от его ЭДС вследствие падения напряжения во внутренних сопротивлениях источника, а напряжения приемника отличаются от напряжений источника за счет падений напряжения в сопротивлениях проводов электрической сети. Для упрощения анализа соотношений в трехфазных цепях будем пренебрегать указанными падениями напряжений.

Применяя второй закон Кирхгофа поочередно ко всем фазам при соединении источников звездой, получим

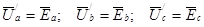. (3)

На основании выражений (3) можно сделать вывод о том, что если генератор имеет симметричную систему ЭДС, то его фазные напряжения тоже симметричны, а векторная диаграмма фазных напряжений (рис. 1.4,а) не отличается от векторной диаграммы ЭДС генератора.

На основании уравнений по второму закону Кирхгофа для контуров N₁abN₁, N₁bcN₁ и N₁caN₁ можно получить следующие уравнения, связывающие линейные и фазные напряжения:

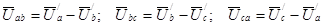. (4)

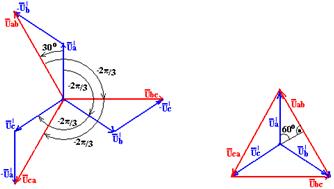
а) б)

Рисунок 1.4

Используя выражения (4) и имея векторы фазных напряжений (рис. 1.4,а), можно построить векторы линейных напряжений U_ab, U_bc, U_ca.

Из векторной диаграммы (рис. 1.4,а) следует, что при соединении источника звездой линейные напряжения равны и сдвинуты по фазе относительно друг друга на угол 2π/3. Векторы линейных напряжений, как правило, изображают соединяющимися векторами соответствующих фазных направлений, как показано на рис. 1.4,б. Из векторной диаграммы (рис. 1.4,б) следует, что

. (5)

Такое соотношение существует между любыми другими линейными и фазными напряжениями. Поэтому можно записать, что вообще при соединении источника звездой

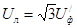. (6)

Выражения (3) справедливы и при соединении источника треугольником (рис. 1.3,б). Непосредственно из схемы следует, что линейные напряжения равны соответствующим фазным напряжениям:

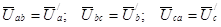. (7)

Можно записать, что при соединении источника треугольником вообще

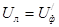. (8)

Векторная диаграмма фазных и линейных напряжений при соединении источника треугольником приведена на рис. 1.5.