Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элементов

Резистивный элемент. Если ток в резистивном элементе синусоидальный

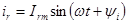, (2.10)

то по закону Ома напряжение, приложенное к элементу равно

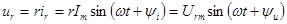, (2.11)

где амплитуды тока и напряжения связаны соотношением

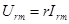, (2.12)

а их начальные фазы одинаковы:

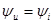, (2.13)

т.е. ток и напряжение в резистивном элементе изменяются синфазно.

Разделив правую и левую части выражения (2.12) на 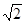, получим соотношение для действующих значений напряжения и тока резистивного элемента:

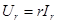. (2.14)

т.е. ток и напряжение в резистивном элементе изменяются синфазно.

Представим синусоидальные ток и напряжение в комплексной форме:

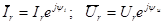. (2.15)

Учитывая (2.13) и (2.14), получим закон Ома в комплексной форме для резистивного элемента:

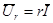. (2.16)

Соотношение между комплексными значениями тока и напряжения для резистивного элемента иллюстрируется векторной диаграммой, приведенной на рис. 2.3.

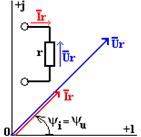
Рисунок 2.3

Индуктивный элемент. Если ток в индуктивном элементе синусоидальный

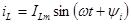, (2.17)

то по закону электромагнитной индукции напряжение на индуктивном элементе равно

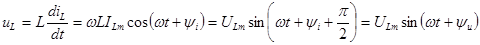, (2.18)

где амплитуды напряжения и тока связаны соотношением

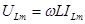, (2.19)

а начальные фазы соотношением

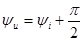. (2.20)

Разделив правую и левую части выражения (2.19) на 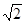, получим соотношение для действующих значений напряжения и тока индуктивного элемента:

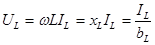. (2.21)

Представим синусоидальные ток i_L и напряжение u_L индуктивного элемента в комплексной форме:

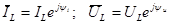. (2.22)

На рис. 2.4 приведена векторная диаграмма для индуктивного элемента. На векторной диаграмме показано, что вектор комплексного значения тока отстает от комплексного значения напряжения на угол π/2.

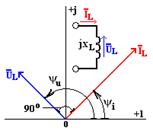
Рисунок 2.4

Пользуясь выражением (2.21) и частными случаями формулы Эйлера

,

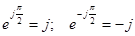получим закон Ома в комплексной форме для индуктивного элемента:

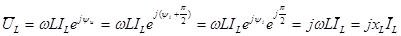. (2.23)

Входящая в полученное выражение величина 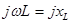называется комплексным сопротивлением индуктивного элемента, а обратная ей величина 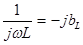- комплексной проводимостью индуктивного элемента.

Емкостной элемент. Если напряжение между выводами емкостного элемента изменяется по синусоидальному закону

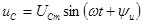, (2.24)

то синусоидальный ток

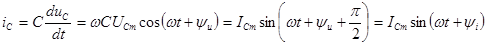, (2.25)

где амплитуды напряжения и тока связаны соотношением

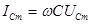, (2.26)

а их начальные фазы – соотношением

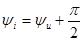. (2.27)

Разделив левую и правую части выражения (2.26) на 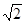, получим соотношение для действующих значений напряжения и тока емкостного элемента:

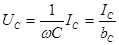. (2.28)

Представим синусоидальные ток и напряжение емкостного элемента соответствующими комплексными значениями:

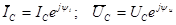. (2.29)

На рис. 2.5 приведена векторная диаграмма для емкостного элемента, из которой видно, что вектор комплексного значения напряжения отстает по фазе от векторного комплексного значения тока на угол π/2.

Учитывая выражения (2.26) и (2.27), получим закон Ома в комплексной форме для емкостного элемента:

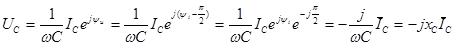. (2.30)

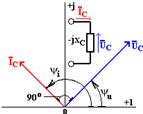
Рисунок 2.5

Величина 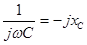, входящая в выражение (2.30), называется комплексным сопротивлением емкостного элемента, а обратная ей величина 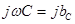- комплексной проводимостью емкостного элемента.