Последовательное соединение элементов в цепи

Рассмотрим цепь, приведенную на рис. 3.1, активное сопротивление которой r, индуктивность L и емкость С.

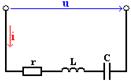
Рисунок 3.1

При напряжении 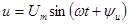в цепи протекает ток 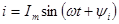. По второму закону Кирхгофа

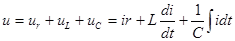. (3.1)

Полученное уравнение преобразуется в дифференциальное уравнение второго порядка, решение которого состоит из общего решения однородного уравнения и частного решения. Общее решение однородного уравнения определяет составляющую переходного процесса, которая имеет место в течение относительно короткого промежутка времени после начала перехода цепи в другое установившееся состояние. Найдем частное решение, определяющее ток в цепи после окончания переходного процесса, когда в ней будет протекать установившийся переменный ток.

Частным решением является выражение синусоидального тока 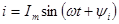, для которого нужно найти амплитуду I_m и фазовый угол ψ_i (или угол сдвига по фазе φ = ψ_u – ψ_i).

На основании уравнения (3.1) можно записать

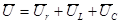. (3.2)

В соответствии с уравнением (3.2) построим векторную диаграмму (рис. 3.2). На выбор исходного вектора 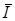не налагается каких-либо условий – направим этот вектор вертикально вверх. Все векторы будем изображать в принятом масштабе.

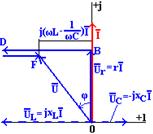
Рисунок 3.2

В фазе с вектором тока 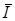находится вектор активной составляющей напряжения 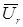. Под углом π/2 в сторону опережения относительно вектора 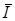направим вектор индуктивной составляющей напряжения 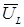, а под углом π/2 в сторону отставания – вектор емкостной составляющей напряжения 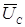. Геометрическая сумма всех векторов действующих величин определит вектор действующего напряжения 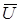на зажимах цепи.

Из прямоугольного треугольника ОBF имеем

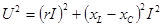. (3.3)

Тогда

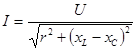. (3.4)

Сдвиг по фазе φ между напряжением и током определится выражением

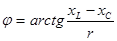. (3.5)

Сопротивление цепи, определяемое формулой

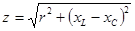, (3.6)

называется полным сопротивлением цепи. Реактивным называется сопротивление x = x_L – x_C. Если в цепи преобладает индуктивное сопротивление, то реактивное сопротивление положительно, разность фаз напряжения и тока положительна (φ > 0) и напряжение цепи опережает ток. Если в цепи преобладает емкостное сопротивление, то реактивное сопротивление отрицательно, разность фаз отрицательна (φ < 0) и ток цепи опережает напряжение.

В подобных цепях угол φ сдвига по фазе может изменяться в пределах .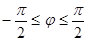

Для комплексных действующих значений можно записать:

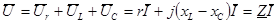. (3.7)

Величина 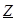является комплексным полным сопротивлением (сопротивлением в символическом виде) и состоит из вещественной и мнимой частей:

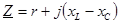. (3.8)

Аналогично закону Ома комплексный ток определяется выражением:

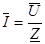. (3.9)

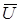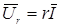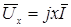Вектор приложенного напряжения можно рассматривать как геометрическую сумму векторов и . Вектор 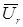совпадает по фазе с вектором тока, а вектор 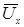перпендикулярен вектору тока.

В полученном треугольнике напряжений 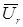находится в фазе с током и называется активной составляющей напряжения:

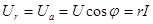. (3.10)

Напряжение 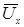сдвинуто по фазе на угол π/2 относительно тока и называется реактивной составляющей напряжения:

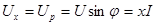. (3.11)

Напряжение на зажимах цепи

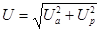. (3.12)

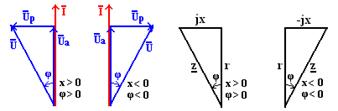
Треугольники напряжений при φ > 0 и φ < 0 представлены соответственно на рис. 3.3,а и 3.3,б.

а) б) в) г)

Рисунок 3.3

Напряжение на зажимах цепи и активное сопротивление всегда положительны. Реактивное напряжение может быть положительным (при φ > 0) или отрицательным (при φ < 0).

Треугольник сопротивлений получается из треугольника напряжений. Треугольники напряжений и сопротивлений подобны. Длины сторон треугольника сопротивлений определяются путем деления соответствующих напряжений на значение тока. Гипотенуза треугольника сопротивлений изображает полное сопротивление цепи, катеты активное и реактивное сопротивления. При φ > 0 сторона треугольника jx направлена влево от катета r – преобладает индуктивное сопротивление; при φ < 0 сторона треугольника –jx направлена вправо – преобладает емкостное сопротивление.

Из треугольника сопротивлений находим соотношения:

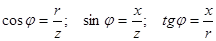. (3.13)