Изображение синусоидально изменяющихся величин векторами на комплексной плоскости

На рис. 2.1 показана комплексная плоскость, на которой можно изображать комплексные числа.

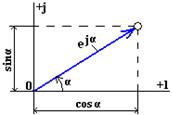
Рисунок 2.1

Комплексное число содержит действительную и мнимую части. По оси абсцисс на комплексной плоскости откладывают действительную часть комплексного числа, а по оси ординат – мнимую. Ось действительных чисел обозначается символом +1, а ось мнимых значений – символом +j. В соответствии с формулой Эйлера

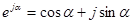. (2.1)

Комплексное число е^jα изображается на комплексной плоскости единичным вектором, составляющим угол α с осью вещественных значений. Угол α отсчитывается против часовой стрелки от оси +1. Модуль функции

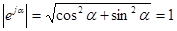. (2.2)

Если вместо функции е^jα взять функцию I_m е^jα, то

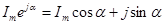. (2.3)

На комплексной плоскости эта функция, так же как и функция е^jα изобразится под углом α к оси +1, но величина вектора будет в I_m больше.

Угол α в формуле (1) может быть любым. Если α = ωt + ψ, т.е. угол изменяется прямо пропорционально времени, то

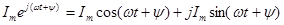. (2.4)

Слагаемое 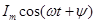представляет собой действительную часть (Re) выражения (2.4):

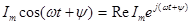. (2.5)

Функция 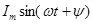есть коэффициент при мнимой части (Im) выражения (2.4):

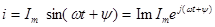. (2.6)

Таким образом, синусоидально меняющийся ток i можно представить как 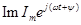, или, что то же самое, как проекцию вращающегося вектора 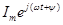на ось +j.

С целью единообразия принято на комплексной плоскости изображать векторы синусоидальных величин, изменяющихся во времени, для момента времени t = 0. При этом вектор 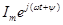равен

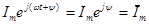, (2.7)

где 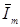– комплексная величина, модуль которой равен I_m, а угол, под которым вектор проведен к оси +1 на комплексной плоскости, равен начальной фазе ψ.

Под комплексом действующего значения тока или под комплексом тока (комплексным током) 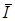понимают

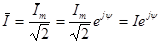. (2.8)