Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию.

а) Смешанное соединение резистивных элементов (рис. 1).

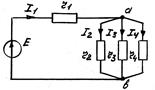
Рисунок 1

Расчет смешанного соединения нужно начинать с определения эквивалентной проводимости g_э каждого параллельного соединения резистивных элементов, подключенных к одной и той же паре узлов.

. (11)

После замены параллельного соединения резистивных элементов, эквивалентным резистивным элементом с сопротивлением:

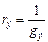. (12)

Получается эквивалентная схема с последовательным соединением двух резистивных элементов r₁ и r₂.

Ток в неразветвленной части цепи:

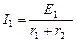. (13)

Чтобы определить токи в параллельных ветвях, нужно сначала вычислить напряжение между узлами a и b.

U_ab = r_э·I₁.

Затем токи в ветвях по закону Ома:

в) Метод преобразования цепей.

В ряде случаев расчет сложной электрической цепи упрощается, если в этой цепи заменить группу резистивных элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе, но в целом после такой замены режим работы остальной части электрической цепи не изменится. Для расчета сложных цепей часто применяется преобразование треугольник – звезда.

с) Метод двух узлов.

Исследуемая цепь часто содержит только два узла или может быть преобразована в подобную цепь. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения).

Так как ветви между узлами а и в соединены параллельно, то напряжение между этими узлами можно выразить через ЭДС ЕК, ток IK и сопротивление rK. По обобщенному закону Ома:

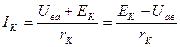. (14)

Тогда

.

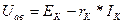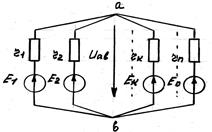
Рисунок 2

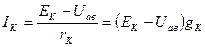, (15)

где - проводимость К-й ветви, U_ав - узловое напряжение.

По первому закону Кирхгофа алгебраическая сумма токов в узле цепи равна нулю, т.е.

.

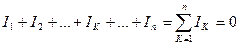Следовательно,

. (16)

Отсюда

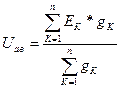. (17)

В полученной формуле со знаком плюс записываются ЭДС, действующие к узлу А.

Основная литература: [1, 3];

Дополнительная литература: [9, 11].