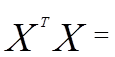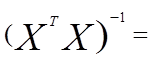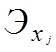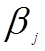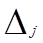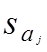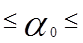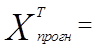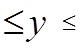Прогнозирование по модели множественной регрессии
Прогнозирование по модели множественной линейной регрессии предполагает оценку ожидаемых значений зависимой переменной при заданных значениях независимых переменных, входящих в уравнение регрессии. Различают точечный и интервальный прогнозы.
Точечный прогноз — это расчетное значение зависимой переменной, полученное подстановкой в уравнение множественной линейной регрессии прогнозных (заданных исследователем) значений независимых переменных. Если заданы значения 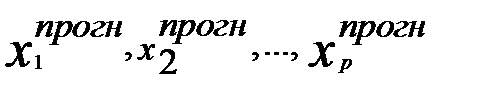 , то прогнозное значение зависимой переменной (точечный прогноз) будет равно
, то прогнозное значение зависимой переменной (точечный прогноз) будет равно
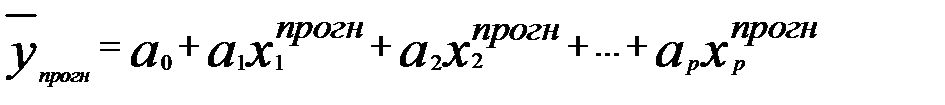 (3.45)
(3.45)
Интервальный прогноз — это минимальное и максимальное значения зависимой переменной, в промежуток между которыми она попадает с заданной долей вероятности и при заданных значениях независимых переменных.
Интервальный прогноз для линейной функции вычисляется по формуле
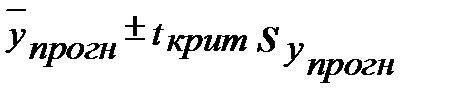 , (3.46)
, (3.46)
где 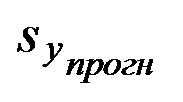 — стандартная ошибка прогноза, вычисляемая по формуле
— стандартная ошибка прогноза, вычисляемая по формуле
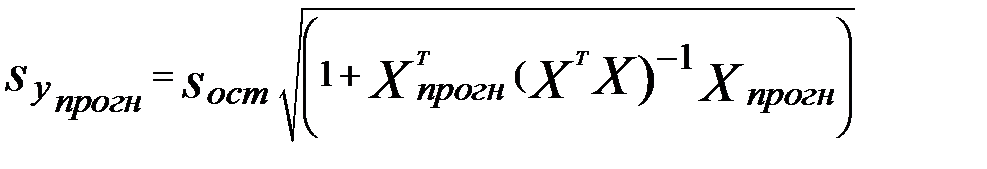 , (3.47)
, (3.47)
где Х— матрица исходных значений независимых переменных; Хпрогн — матрица-столбец прогнозных значений независимых переменных вида
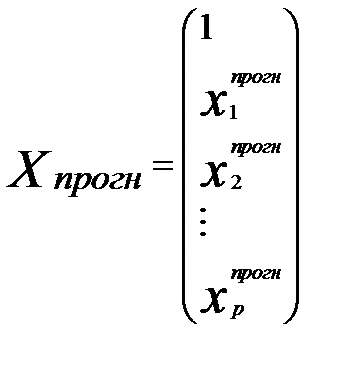 (3.48)
(3.48)
Для сравнения роли различных факторов в формировании моделируемого показателя определяется коэффициент эластичности ( 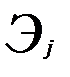 ) или
) или 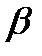 - коэффициент (
- коэффициент ( 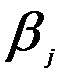 ). Частный коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак у с изменением признака-фактора
). Частный коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак у с изменением признака-фактора 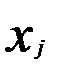 на 1%, и определяется по формуле
на 1%, и определяется по формуле
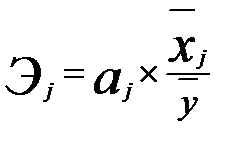 , (3.49)
, (3.49)
где 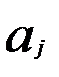 — коэффициент регрессии при
— коэффициент регрессии при 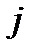 - ом факторе.
- ом факторе.
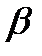 -коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный показатель при изменении соответствующего фактора
-коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный показатель при изменении соответствующего фактора 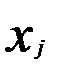 на величину его среднего квадратического отклонения; его формула имеет вид:
на величину его среднего квадратического отклонения; его формула имеет вид:
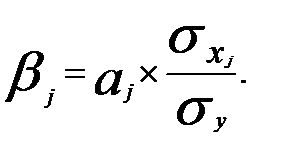 (3.50)
(3.50)
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта – коэффициентов 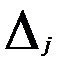 :
:
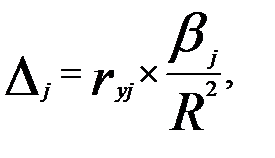 (3.52)
(3.52)
.
Пример
Имеются статистические данные о значениях четырех показателей в разрезе 48 субъектов РФ, которые приведены в табл. 3.3:
1. Поступление налогов, сборов и иных обязательных платежей в консолидированный бюджет РФ (без поступлений ЕСН) в 2009 г., млн. руб.
2. Количество занятых в Российской Федерации в 2009 г., тыс. человек.
3. Объем отгруженных товаров собственного производства, выполненных работ и оказанных услуг собственными силамипо виду экономической деятельности «Обрабатывающие производства» в Российской Федерации в 2009 г., млн руб.
4.Объем отгруженных товаров собственного производства, выполненных работ и услуг собственными силами по виду экономической деятельности «Производство и распределение электроэнергии, газа и воды» в Российской Федерации в 2009 г., млн. руб.
Предположим, что зависимой переменной у в данном случае является «поступление налогов, сборов и иных обязательных платежей в консолидированный бюджет РФ». Для краткости будем называть эту переменную «поступление налогов». Независимыми переменными являются остальные три переменные, которые будем называть и обозначать как «количество занятых» X1; «отгрузка в обрабатывающих производствах»X2, «производство энергии»X3. Допустим также, что связь между зависимой и независимыми переменными может быть выражена в виде линейной функции регрессии
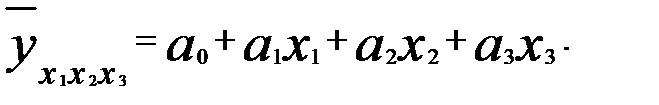 (3.53)
(3.53)
Некоторые экономические показатели деятельности
субъектов РФ в 2009 г.
Таблица 3.3
| № п/п | Субъект РФ | Поступление налогов, млн. руб. | Количество занятых, тыс. человек | Отгрузка в обрабатывающих производствах, млн. руб. | Производство энергии, млн руб. |
| У | X1 | X2 | X3 | ||
| Республика Ингушетия | 1422,2 | 107,2 | |||
| Еврейская автономная область | 2529,7 | 82,3 | |||
| Республика Тыва | 2629,1 | 101,6 | |||
| Республика Алтай | 2764,3 | 87,6 | |||
| Карачаево-Черкесская Республика | 3347,5 | 188,3 | 10 921 | ||
| Республика Калмыкия | 3914,2 | 121,9 | |||
| Республика Адыгея | 4400,8 | 187,1 | 12 565 | ||
| Республика Северная Осетия — Алания | 326,5 | 11 088 | |||
| Магаданская область | 6956,7 | 97,1 | |||
| Кабардино-Балкарская Республика | 7595,1 | 352,5 | 17 609 | ||
| Республика Хакасия | 9257,8 | 254,7 | 39 640 | 17 634 | |
| Чукотский автономный округ | 9317,1 | 30,5 | |||
| Республика Марий Эл | 9978,8 | 323,7 | 46 180 | ||
| Псковская область | 10 144,80 | 323,3 | 32 074 | ||
| Чеченская Республика | 10 215,40 | ||||
| Республика Карелия | 11 349,50 | 337,8 | 39 962 | 14 684 | |
| Курганская область | 12 046,90 | 38 308 | 12 093 | ||
| Республика Мордовия | 12 061,40 | 65 507 | |||
| Костромская область | 12 104,20 | 340,9 | 50 532 | 20 922 | |
| Камчатский край | 13 042,40 | 11 245 | 12 721 | ||
| Орловская область | 13 104,30 | 38 089 | |||
| Ивановская область | 13 396,40 | 491,2 | 42 865 | 18 506 | |
| Республика Дагестан | 14 170,30 | 1104,1 | 21 031 | 12 573 | |
| Тамбовская область | 14 227,00 | 499,5 | 47 738 | ||
| Новгородская область | 16 868,50 | 322,5 | 80 915 | ||
| Республика Бурятия | 18 019,40 | 392,3 | 29 660 | 12 532 | |
| Смоленская область | 18 950,30 | 505,4 | 78 278 | 43 604 | |
| Курская область | 19 995,50 | 536,5 | 67 241 | 43 733 | |
| Забайкальский край | 20 445,60 | 13 687 | |||
| Липецкая область | 21 220,80 | 575,5 | 228 812 | 17 311 | |
| Ульяновская область | 21 360,00 | 619,1 | 76 523 | 16 471 | |
| Пензенская область | 21 418,80 | 634,3 | 71 307 | 12 061 | |
| Кировская область | 21 477,10 | 76 151 | 20 857 | ||
| Чувашская Республика | 21 816,30 | 608,4 | 85 926 | 17 071 | |
| Астраханская область | 22 824,90 | 475,8 | 34 576 | 10 532 | |
| Брянская область | 23 579,30 | 569,8 | 57 187 | 10 519 | |
| Амурская область | 23 702,60 | 417,3 | 16 412 | 16 512 | |
| Калужская область | 24 007,20 | 530,5 | 161 769 | 10 369 | |
| Тульская область | 27 581,20 | 746,6 | 182 031 | 24 376 | |
| Вологодская область | 28 057,50 | 617,8 | 236 267 | 23 180 | |
| Алтайский край | 29 815,50 | 1125,5 | 115 197 | 24 804 | |
| Тверская область | 32 236,50 | 687,4 | 103 158 | 44 961 | |
| Белгородская область | 32 657,40 | 754,9 | 233 608 | 18 773 | |
| Владимирская область | 32 672,70 | 688,4 | 142 867 | 20 093 | |
| Мурманская область | 34 351,10 | 482,2 | 49 081 | 34 395 | |
| Воронежская область | 36 050,40 | 1042,4 | 125 343 | 39 170 | |
| Рязанская область | 36 544,30 | 95 522 | 23 932 | ||
| Калининградская область | 37 136,90 | 459,5 | 147 573 | 15 429 |
Источник: данные Росстата.
Применяя к исходным данным (см. табл. 3.3) МНК, оценим параметры регрессии. Система нормальных уравнений имеет вид
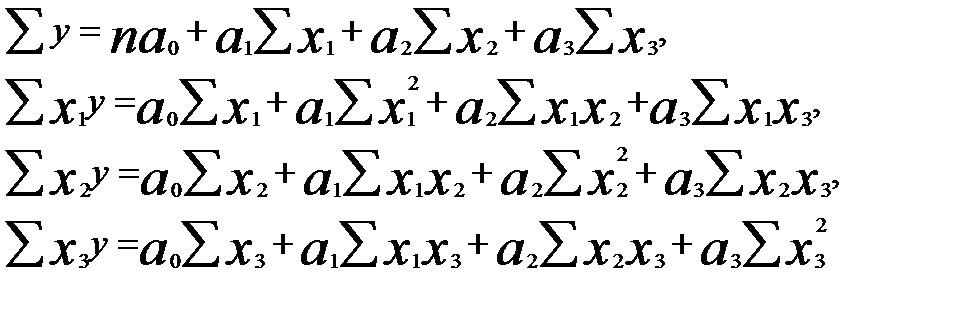 (3.54)
(3.54)
Произведение матриц 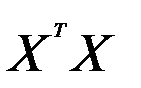 в данном примере имеет вид:
в данном примере имеет вид:
| 21591,9 | ||||||
|
| 21591,9 | 12748269,45 | 403092447,4 | |||
| 3,83901E+11 | ||||||
| 403092447,4 |
(3.55)
Отметим, что в матрице (3.55) приведены значения коэффициентов при параметрах 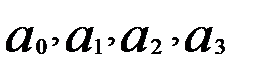 системы (3.54).
системы (3.54).
Обратная матрица от (3.55):
| 0,090330662 | -0,000135839 | 6,71354E-08 | -8,46746E-07 | |||
|
| -0,000135839 | 6,45061E-07 | -1,05161E-09 | -5,8789E-09 | ||
| 6,71354E-08 | -1,05161E-09 | 8,48229E-12 | -8,77047E-12 | |||
| -8,46746E-07 | -5,8789E-09 | -8,77047E-12 | 2,71022E-10 |
(3.56)
Значения параметров системы (3.54) приведены в табл. (3.4)
Таблица 3.4
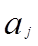
| |||
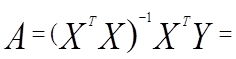
| 3226,441 | ||
| 12,448 | |||
| 0,060 | |||
| 0,310 |
(3.57)
Уравнение регрессии имеет следующий вид
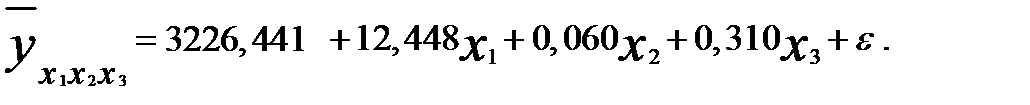 (3.58)
(3.58)
Из уравнения регрессии следует, что между сбором налогов и независимыми переменными, входящими в модель, наблюдается прямая связь. Напомним, что коэффициенты при независимых переменных называются коэффициентами регрессии. Они являются абсолютными показателями силы связи и характеризуют среднее изменение зависимой переменной при единичном изменении независимой переменной — сомножителя данного коэффициента при условии неизменности остальных независимых переменных, включенных в уравнение (модель) регрессии.
Значения коэффициентов 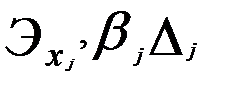 приведены в табл. 3.5
приведены в табл. 3.5
Таблица 3.5
| 0,324 | 0,220 | 0,268 | |
| 0,307 | 0,373 | 0,340 | |
|
| 0,308 | 0,366 | 0,325 |
Сопоставляя полученные коэффициенты, можно сделать вывод о том,что наиболее сильное влияние на сбор налогов оказывает фактор 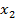 .
.
Стандартные ошибки коэффициентов регрессии 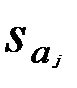 определены по соотношениями (3.57):
определены по соотношениями (3.57):
Таблица 3.6
|
| 1651,796 | 4,414 | 0,016 | 0,090 |
Значимости коэффициентов регрессии проверим по t-критерию Стьюдента
| 1,95 | 2,82 | 3,76 | 3,43 |
Учитывая, что выполняется условие 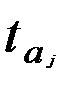 >
> 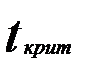 все коэффициенты, кроме
все коэффициенты, кроме 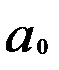 , являются значимыми, где
, являются значимыми, где 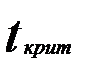 =2,0153.
=2,0153.
Границы доверительных интервалов для коэффициентов регрессии следующие:
| -102,536 |
| 6555,417 | |
| 3,552 | 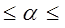 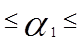
| 21,344 | |
| 0,028 | 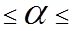
| 0,092 | |
| 0,128 | 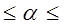 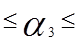
| 0,493 |
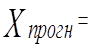
| ||
| |||||
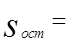
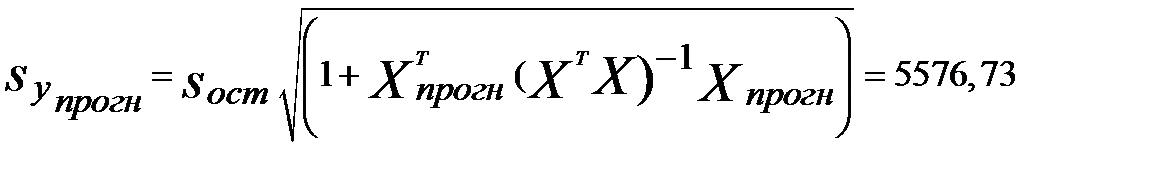
|
| 5495,901163 |
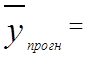
| 18012,93 |
| tкрит= | 2,0153 |
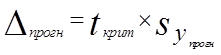
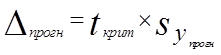
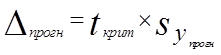
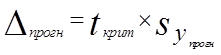
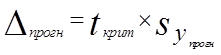
|
| =11198,48 |
| 6814,45 |
| 29211,41 |
Для получения таблиц регрессионной статистики и дисперсионного анализа воспользуемся режимом “Регрессия” EXCEL (табл.3.7 и 3.8 ).
Регрессионная статистика
Таблица 3.7
| Множественный R | 0,856 |
| R-квадрат | 0,733 |
| Нормированный R-квадрат | 0,715 |
| Стандартная ошибка | 5495,901 |
| Наблюдения |
Дисперсионный анализ
Таблица 3.8
| df | SS | MS | F | Значимость F | |
| Регрессия | 40,31035571 | 1,10224E-12 | |||
| Остаток | 30204929,59 | ||||
| Итого |
Дата добавления: 2016-03-22; просмотров: 5707;