Фиктивные переменные

При изучении экономических взаимосвязей возникает необходимость

учесть в модели влияние качественного фактора (фактора, не имеющего количественного выражения), например пол потребителя, фактор сезонности, наличие государственных программ. Влияние качественных признаков может приводить к скачкообразному изменению параметров линейных регрессионных моделей, построенных для различных значений качественного признака. Такие модели называются регрессионными моделями с переменной структурой.

Чтобы учесть влияние качественного фактора в рамках одного регрессионного уравнения вводятся, так называемые, фиктивные переменные с двумя значениями 0 и 1. Например, изучается зависимость потребления товара y от величины дохода x с учетом пола потребителя. С использованием фиктивной переменной z

уравнение регрессии принимает вид

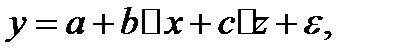. (3.52)

Вводя новый член регрессии c*z , тем самым предполагаем, что пол

потребителя влияет только на величину свободного члена уравнения (параметрa характеризует объем потребления). Чтобы учесть влияние пола потребителяна величину коэффициента регрессии b (характеризующего «склонность» к потреблению), следует в модель регрессии ввести дополнительное слагаемое

d*z*x , что дает

y=a+b*x+c*z+d*z*x+ԑ. (3.53)

Таким образом, модель (3.69) является объединением двух моделей для

мужчин и женщин

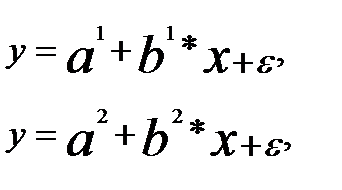
где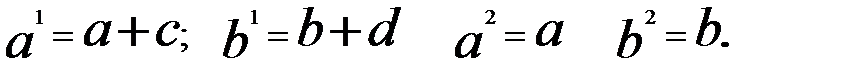

Проверка значимости коэффициентов при фиктивных факторах z и z·x покажет значимость влияния качественного показателя на изучаемый признак инеобходимость включения в уравнение регрессии соответствующего члена.

Если качественный признак имеет более двух градаций признака, то вводится несколько фиктивных переменных, число которых на единицу меньшечисла градаций признака. Например, чтобы учесть сезонность, вводятся трификтивные переменные

(3.54)

и уравнение регрессии примет вид

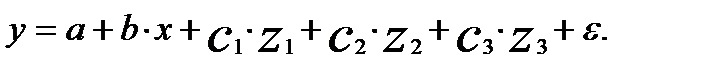
Если качественных признаков несколько, то фиктивные переменные вводятся для каждого признака по таким же правилам.

Тест Чоу

Предположим, что имеется две набора наблюдений за совместным изменением двух зависимой и объясняющей переменной (xi,yi), полученные в различных условиях. Возникает вопрос можно ли считать две полученные выборкинаблюдений частями одной объединенной выборки или принципиально различными, для которых уравнения регрессии должны строиться отдельно. Ответ на этот вопрос дается с помощью теста Чоу.

Рассмотрим уравнения регрессии, построенные по первой, второй и объединенной выборкам

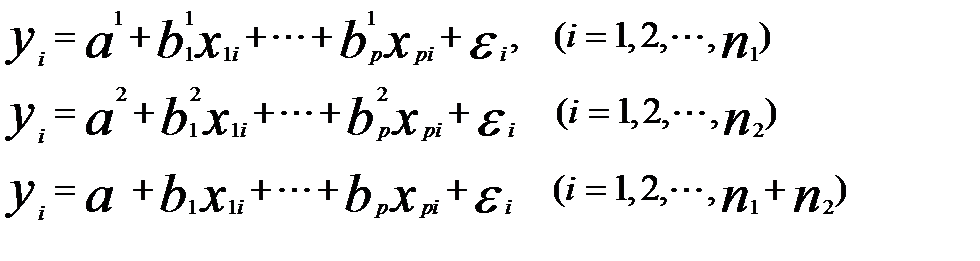
Обозначим суммы квадратов остатков регрессии, полученных по первой,второй и объединенной выборкам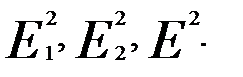

Согласно тесту Чоу, нулевая гипотеза H0 о том, что две выборки являютсячастями одной объединенной выборки, отвергается при уровне значимости α,если выполняется условие

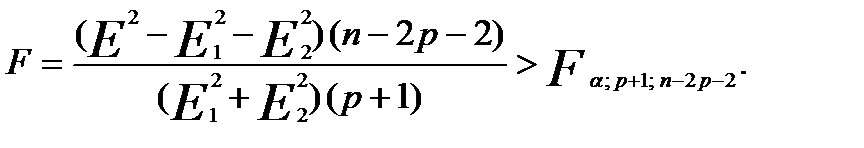
Лекция № 4