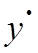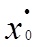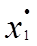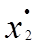Обобщенный метод наименьших квадратов
Обобщенный метод наименьших квадратов (ОМНК) применяется в тех случаях, когда нарушены условия Гаусса — Маркова, касающиеся характера случайных остатков, а именно:
— гомоскедастичность (постоянство дисперсии) случайных остатков;
— некоррелированность остатков между собой. Нарушение этих условий означает, что ковариационная матрица остатков  не является скалярной. Она будет иметь вид
не является скалярной. Она будет иметь вид
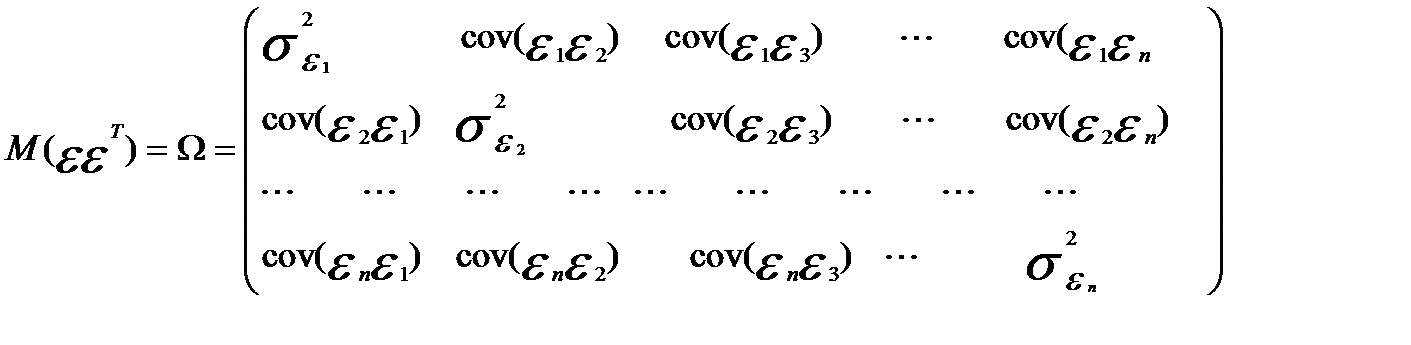 (3.60)
(3.60)
На главной диагонали этой матрицы расположены дисперсии случайных остатков для различных наблюдений (i = 1 -п),не одинаковые по своей величине. Ковариации случайных остатков 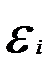 и
и 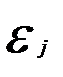 в общем случае также ненулевые. Если остальные условия построения классической нормальной линейной модели выполняются, то модель
в общем случае также ненулевые. Если остальные условия построения классической нормальной линейной модели выполняются, то модель
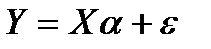 (3.61)
(3.61)
называется обобщенной линейной моделью.
Напомним, что формула для расчета вектора - столбца неизвестных параметров с помощью обычного МНК в матричной форме имеет вид.
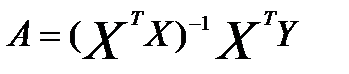
Сущность обобщенного метода наименьших квадратов состоит в том, чтобы устранить нарушения предпосылок МНК, «скорректировав» расчеты параметров уравнения регрессии с учетом значений ковариационной матрицы остатков. Такая «корректировка» может быть проведена с использованием формулы
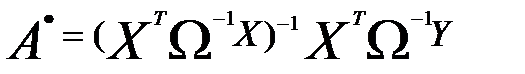 ), (3.62)
), (3.62)
где  — ковариационная матрица остатков.
— ковариационная матрица остатков.
Доказательство эффективности оценок, полученных с помощью обобщенного МНК (ОМНК), содержатся в теореме Айткена.
Теорема Айткена. В классе линейных несмещенных оценок вектора A для обобщенной линейной модели оценка 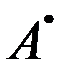 имеет наименьшую ковариационную матрицу.
имеет наименьшую ковариационную матрицу.
Следовательно, ОМНК- оценка является несмещенной. Ковариационная матрица случайных остатков  является невырожденной симметричной матрицей, поэтому она может быть представлена через некую невырожденную матрицу Р следующим образом:
является невырожденной симметричной матрицей, поэтому она может быть представлена через некую невырожденную матрицу Р следующим образом:
 = РРТ.(3.63)
= РРТ.(3.63)
В свою очередь, обратная матрица 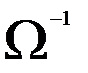 может быть выражена как
может быть выражена как
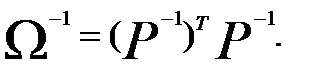 (3.64)
(3.64)
Запишем формулу оценок параметров линейной регрессии по ОМНК, используя вместо матрицы  матрицу Р.
матрицу Р.
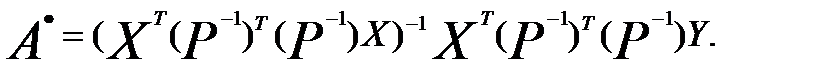 (3.65)
(3.65)
Если произвести замену переменных
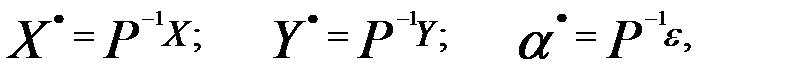 (3.66)
(3.66)
то оценка 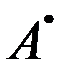 будет иметь вид оценки параметров по обычному МНК:
будет иметь вид оценки параметров по обычному МНК:
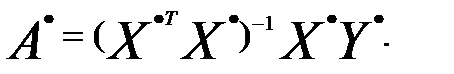 (3.67)
(3.67)
Иначе говоря, если преобразовать переменные X и Y по формулам, то применение к ним обычного МНК приведет к тому же результату, что и применение ОМНК к исходным переменным.
Преобразование переменных приводит к следующему виду обобщенной модели регрессии:
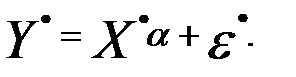
Получены два способа применения ОМНК: с использованием ковариационной матрицы остатков  и формулы (3.62) и с использованием матрицы Р и модели с преобразованными переменными (3.65), для решения которой достаточно применить обычный МНК.
и формулы (3.62) и с использованием матрицы Р и модели с преобразованными переменными (3.65), для решения которой достаточно применить обычный МНК.
Если предпосылки МНК о гомоскедастичности и некоррелированности остатков выполняются, то матрица  превращается в скалярную и обобщенный метод наименьших квадратов дает тот же результат, что и обычный МНК.
превращается в скалярную и обобщенный метод наименьших квадратов дает тот же результат, что и обычный МНК.
Основная проблема, возникающая при использовании ОМНК, заключается в том, что фактические значения элементов матрицы  неизвестны. Поэтому для применения этого метода используют их оценки, полученные на основе исследования имеющихся в распоряжении данных. В этом случае говорят о доступном ОМНК.
неизвестны. Поэтому для применения этого метода используют их оценки, полученные на основе исследования имеющихся в распоряжении данных. В этом случае говорят о доступном ОМНК.
Для оценки элементов ковариационной матрицы остатков  выдвигают разные предположения об их характере и структуре.
выдвигают разные предположения об их характере и структуре.
Как правило, считают, что гетероскедастичность остатков присуща данным пространственных выборок, а автокорреляция остатков — временным рядам. Поэтому в зависимости от характера исходных данных часто предполагают или гетероскедастичность остатков при условии отсутствия автокорреляции, или их автокорреляцию при условии гомоскедастичности.
Если остатки только гетероскедастичны, ковариационная матрица остатков
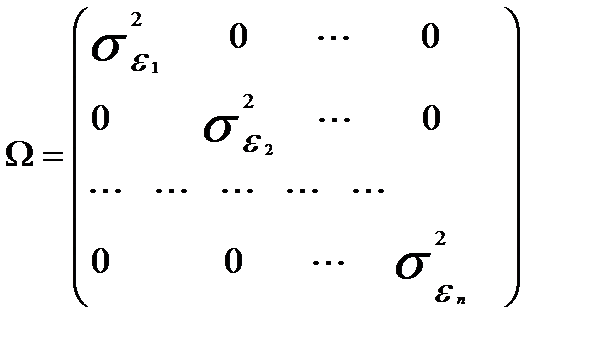 (3.68)
(3.68)
Таким образом, следует дать оценку не всем элементам матрицы  , а только ее п элементам, стоящим на главной диагонали.
, а только ее п элементам, стоящим на главной диагонали.
Обобщенный метод наименьших квадратов можно с учетом матрицы (3.568 записать в виде системы нормальных уравнений
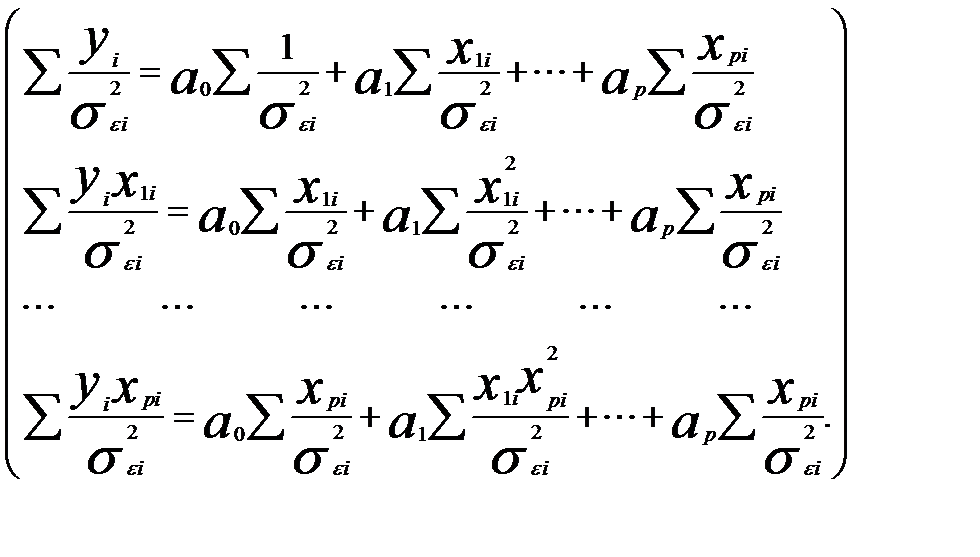
В данной системе переменные и их попарные произведения называют еще
методом взвешенных наименьших квадратов. Подчеркнем, что весовой коэффициент значений исходных переменных х и у для каждого номера наблюдения будет свой. То есть для первого наблюдения все переменные делятся на 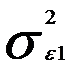 , для второго — на
, для второго — на 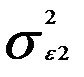 , для последнего, n-го наблюдения,— на
, для последнего, n-го наблюдения,— на 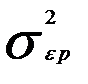 .
.
В качестве оценок дисперсий случайных остатков можно использовать квадраты остатков, полученных при применении обычного МНК.
Процедура применения ОМНК в данном случае предполагает следующие шаги:
к исходным данным применяется обычный МНК и вычисляются случайные остатки 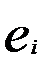 ;
;
делаются предположения относительно функциональной зависимости дисперсии случайных остатков от каких-либо переменных:
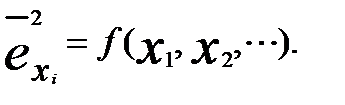 (3.69)
(3.69)
В качестве функции, может, например, использоваться функция по тесту Уайта
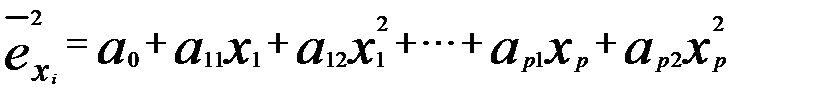
или любая другая аналогичная функция;
с помощью МНК находят параметры модели (3.69), используя в качестве фактических значений зависимой переменной случайные остатки 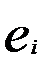 , найденные на первом шаге;
, найденные на первом шаге;
по модели (3.69 рассчитывают выровненные значения случайных остатков 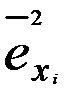 . Эти значения рассматривают как оценки неизвестных дисперсий случайных остатков
. Эти значения рассматривают как оценки неизвестных дисперсий случайных остатков 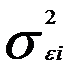 , т.е. диагональных элементов матрицы (3.68);
, т.е. диагональных элементов матрицы (3.68);
определяют параметры множественной линейной регрессии с помощью ОМНК в зависимости от алгоритма, выбранного для расчета параметров: по формуле (3.46) или с использованием преобразованных переменных с применением к ним обычного МНК. В последнем случае возникает вопрос о виде матрицы (Р-1).
Так как в рассматриваемом случае матрица  имеет только диагональные элементы, то обратная к ней матрица
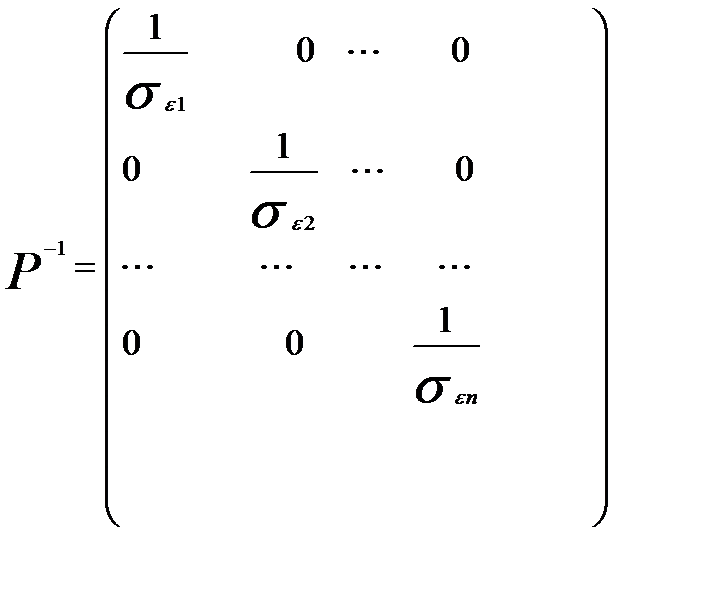
имеет только диагональные элементы, то обратная к ней матрица 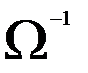 также является диагональной и имеет вид
также является диагональной и имеет вид
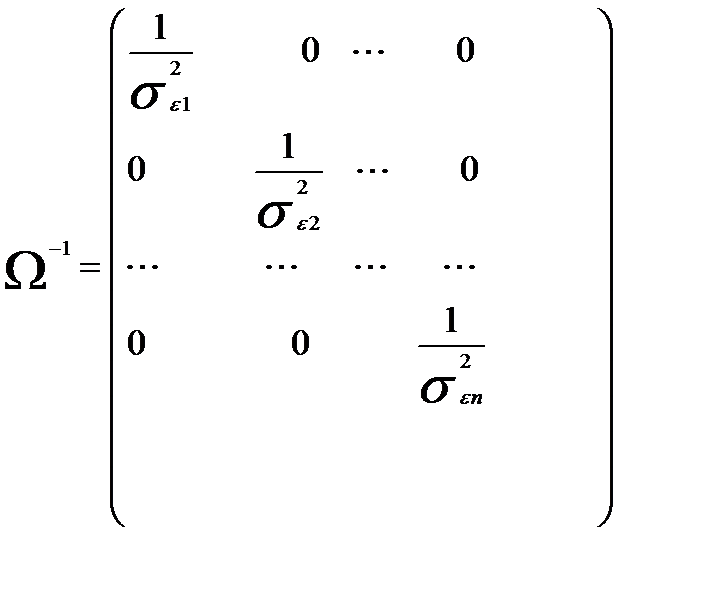
Тогда матрица 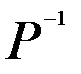 равна
равна
С учетом преобразования переменных уравнение множественной линейной регрессии будет иметь вид
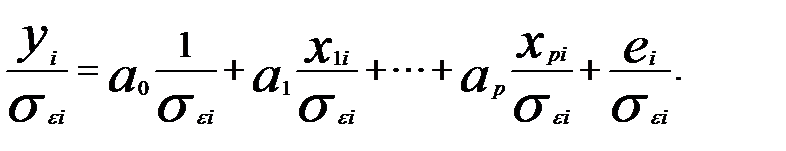
Отметим, что полученное уравнение регрессии не имеет свободного члена.
Применение ОМНК для случая гетероскедастичности остатков еще более упрощается, если предполагается зависимость дисперсии случайных остатков от квадратов значения какой-то одной переменной 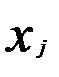 :
:
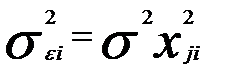 ,
,
где 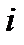 - номер наблюдения; j – номер переменной.
- номер наблюдения; j – номер переменной.
В этом случае ковариционная матрица остатков будет иметь вид
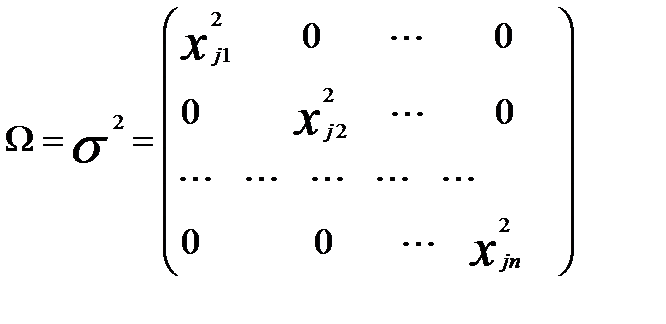
Диагональные элементы матрицы Q уже известны и равны квадратам фактических значений переменной 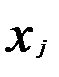 . Постоянный множитель
. Постоянный множитель 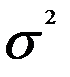 при расчётах по формуле (3.46) сокращается, поэтому матрицу
при расчётах по формуле (3.46) сокращается, поэтому матрицу  можно заменить матрицей
можно заменить матрицей 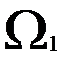 без этого множителя
без этого множителя
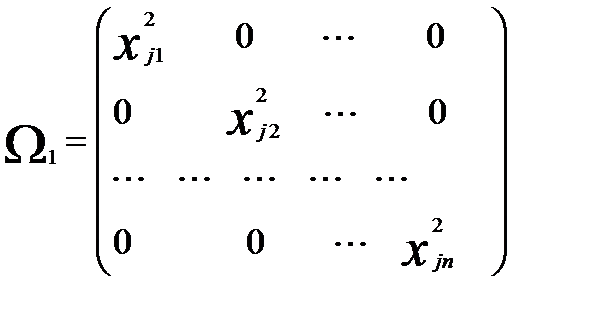 .
.
Матрица 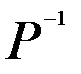 в этом случае равна
в этом случае равна
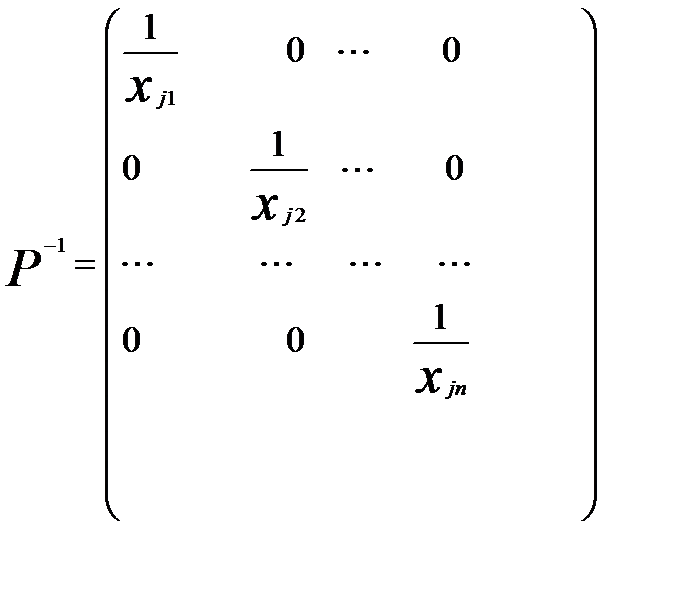 .
.
Использование значений какой-либо независимой переменной в качестве основы для оценки ковариационной матрицы остатков позволяет дать экономическую интерпретацию результатов, полученных по ОМНК.
Как было выявлено ранее, случайные остатки в модели регрессии
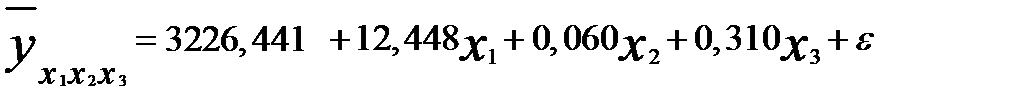
гетероскедастичны, корень из дисперсии случайных остатков и значения независимой переменной х3 связаны линейно. То есть мы можем предположить, что 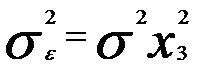 .
.
В этом случае можно применить метод взвешенных наименьших квадратов, разделив каждую переменную, входящую в уравнение регрессии, на соответствующее значение переменной х3:
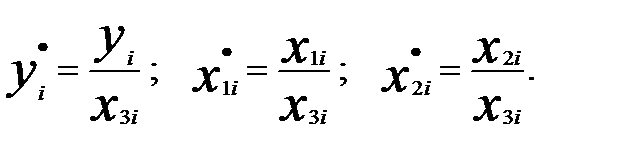
Преобразование переменных затронет также столбец множителей - единиц при свободном члене
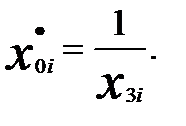
Модель с преобразованными переменными будет иметь вид
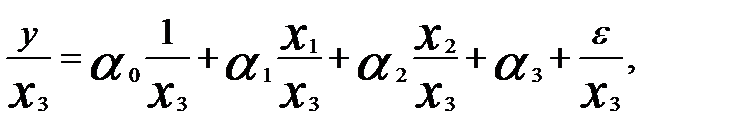
или
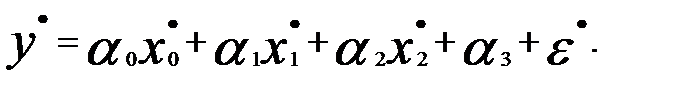
Ниже приведена табл. 3.9, содержащая преобразованные переменные по данным примера 1.
Преобразование переменных при применении ОМНК для модели регрессии поступления налогов от количества занятых, объема отгрузки в обрабатывающих производствах и производства энергии
Таблица 3.9
| № п/п | Субъект РФ |
|
|
|
| ||||
| Республика Ингушетия | 1,940 | 0,00136 | 0,146 | 0,363 | |||||
| Еврейская автономная область | 1,240 | 0,00049 | 0,040 | 1,404 | |||||
| Республика Тыва | 1,300 | 0,00049 | 0,050 | 0,213 | |||||
| Республика Алтай | 2,351 | 0,00085 | 0,074 | 1,044 | |||||
| Карачаево-Черкесская Республика | 0,783 | 0,00023 | 0,044 | 2,555 | |||||
| Республика Калмыкия | 2,618 | 0,00067 | 0,082 | 0,621 | |||||
| Республика Адыгея | 1,467 | 0,00033 | 0,062 | 4,188 | |||||
| Республика Северная Осетия — Алания | 1,769 | 0,00030 | 0,098 | 3,323 | |||||
| Магаданская область | 0,838 | 0,00012 | 0,012 | 0,299 | |||||
| Кабардино-Балкарская Республика | 1,312 | 0,00017 | 0,061 | 3,041 | |||||
| Республика Хакасия | 0,525 | 0,00006 | 0,014 | 2,248 | |||||
| Чукотский автономный округ | 1,496 | 0,00016 | 0,005 | 0,085 | |||||
| Республика Марий Эл | 1,332 | 0,00013 | 0,043 | 6,166 | |||||
| Псковская область | 1,799 | 0,00018 | 0,057 | 5,687 | |||||
| Чеченская Республика | 1,656 | 0,00016 | 0,058 | 0,094 | |||||
| Республика Карелия | 0,773 | 0,00007 | 0,023 | 2,721 | |||||
| Курганская область | 0,996 | 0,00008 | 0,032 | 3,168 | |||||
| Республика Мордовия | 1,650 | 0,00014 | 0,060 | 8,959 | |||||
| Костромская область | 0,579 | 0,00005 | 0,016 | 2,415 | |||||
| Камчатский край | 1,025 | 0,00008 | 0,015 | 0,884 | |||||
| Орловская область | 1,363 | 0,00010 | 0,039 | 3,963 | |||||
| Ивановская область | 0,724 | 0,00005 | 0,027 | 2,316 | |||||
| Республика Дагестан | 1,127 | 0,00008 | 0,088 | 1,673 | |||||
| Тамбовская область | 1,494 | 0,00011 | 0,052 | 5,013 | |||||
| Новгородская область | 1,877 | 0,00011 | 0,036 | 9,002 | |||||
| Республика Бурятия | 1,438 | 0,00008 | 0,031 | 2,367 | |||||
| Смоленская область | 0,435 | 0,00002 | 0,012 | 1,795 | |||||
| Курская область | 0,457 | 0,00002 | 0,012 | 1,538 | |||||
| Забайкальский край | 1,494 | 0,00007 | 0,035 | 0,578 | |||||
| Липецкая область | 1,226 | 0,00006 | 0,033 | 13,218 | |||||
| Ульяновская область | 1,297 | 0,00006 | 0,038 | 4,646 | |||||
| Пензенская область | 1,776 | 0,00008 | 0,053 | 5,912 | |||||
| Кировская область | 1,030 | 0,00005 | 0,033 | 3,651 | |||||
| Чувашская Республика | 1,278 | 0,00006 | 0,036 | 5,033 | |||||
| Астраханская область | 2,167 | 0,00009 | 0,045 | 3,283 | |||||
| Брянская область | 2,242 | 0,00010 | 0,054 | 5,437 | |||||
| Амурская область | 1,435 | 0,00006 | 0,025 | 0,994 | |||||
| Калужская область | 2,315 | 0,00010 | 0,051 | 15,601 | |||||
| Тульская область | 1,131 | 0,00004 | 0,031 | 7,468 | |||||
| Вологодская область | 1,210 | 0,00004 | 0,027 | 10,193 | |||||
| Алтайский край | 1,202 | 0,00004 | 0,045 | 4,644 | |||||
| Тверская область | 0,717 | 0,00002 | 0,015 | 2,294 | |||||
| Белгородская область | 1,740 | 0,00005 | 0,040 | 12,444 | |||||
| Владимирская область | 1,626 | 0,00005 | 0,034 | 7,110 | |||||
| Мурманская область | 0,999 | 0,00003 | 0,014 | 1,427 | |||||
| Воронежская область | 0,920 | 0,00003 | 0,027 | 3,200 | |||||
| Рязанская область | 1,527 | 0,00004 | 0,022 | 3,991 | |||||
| Калининградская область | 2,407 | 0,00006 | 0,030 | 9,565 |
По преобразованным данным получена следующая модель:
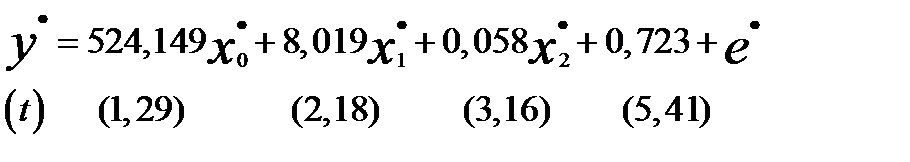
Все коэффициенты полученной модели значимы (табличное значение критерия Стьюдента равно 2,015 ( 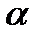 = 0,05; df= = 44)). В данном уравнении параметр при переменной
= 0,05; df= = 44)). В данном уравнении параметр при переменной 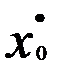 является свободным членом исходной модели, а параметр, равный 0,723, — коэффициентом регрессии при переменной
является свободным членом исходной модели, а параметр, равный 0,723, — коэффициентом регрессии при переменной 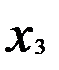 . Таким образом, в исходном виде уравнение регрессии будет иметь вид
. Таким образом, в исходном виде уравнение регрессии будет иметь вид
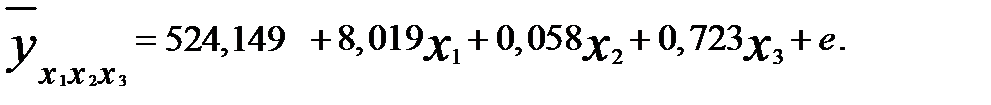
Сопоставив полученное уравнение с исходным
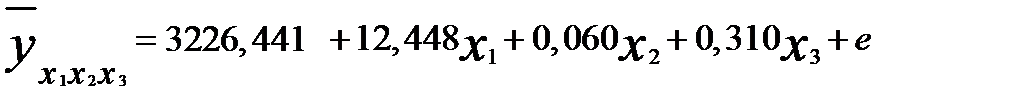
можно отметить существенное изменение практически всех параметров.
Анализ случайных остатков нового уравнения также проведем по тесту Гольфельда – Квандта. Все расчётные значения критерия Фишера получились меньше критического, следовательно нет оснований отвергнуть гипотезу о гомоскедастичности остатков.
Дата добавления: 2016-03-22; просмотров: 6179;