Проверка качества уравнения регрессии. F-критерий Фишера

Как и в случае парной регрессии для оценки качества полученного множественной уравнения регрессии (3.6) можно использовать коэффициентмножественной детерминации, представляющий собой отношение факторной суммы квадратов остатков к их общей сумме квадратов:

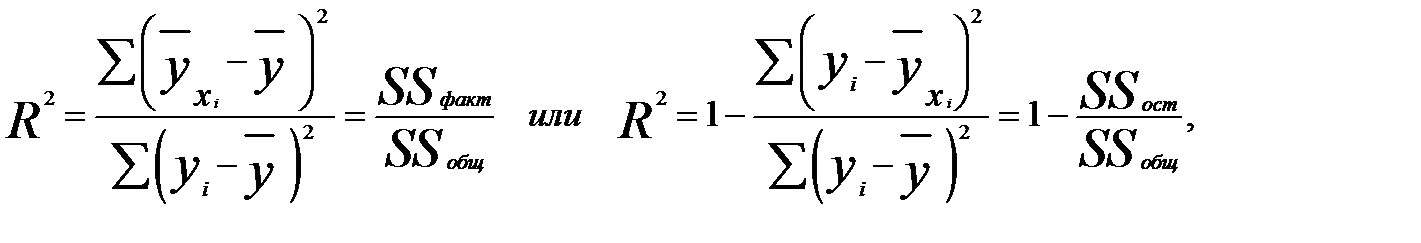(3.35)

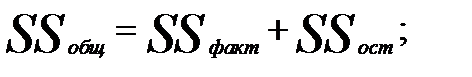
- остаточная сумма квадратов.

Коэффициент множественной корреляции равен корню из коэффициента множественной детерминации:

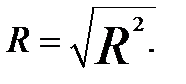(3.36)

Оба показателя изменяются от нуля до единицы. 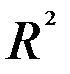показывает, какая часть вариации результативного признака y объяснена уравнением регрессии. Чем выше значение 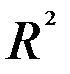, тем лучше данная модель согласуется с данными наблюдений.

Коэффициент множественной корреляции R используется для оценки тесноты связи факторов с исследуемым признаком. Чем ближе величина R к единице, тем теснее данная связь, тем лучше теоретическая зависимость согласуется с эмпирическими данными.

Введём понятие дисперсии на одну степень свободы (df).

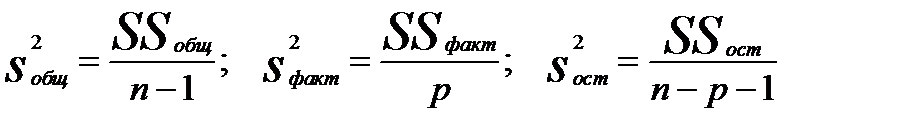, (3.37)

где (n-1) - количество степеней свободы для общей дисперсии;

p–для факторнойдисперсии (количество независимых переменных в уравнении регрессии);

(n-p-1) – для остаточной дисперсии.

Оценка статистической значимости уравнения регрессии (а также коэффициента детерминации 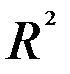) осуществляется с помощью F-критерия Фишера

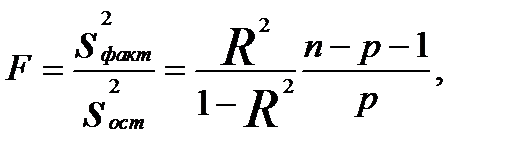(3.38)

Согласно F-критерию Фишера, выдвигаемая «нулевая» гипотеза H0 о статистической незначимости уравнения регрессии отвергается при выполнении условия F >Fкрит, где Fкрит определяется по таблицам F-критерия Фишера по двум степеням свободы k1 = p, k2 = n-p-1 и заданному уровню значимости α.

Величина коэффициента множественной корреляции R не может быть меньше максимального парного индекса корреляции max .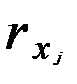

В случае линейной зависимости (3.6) коэффициент корреляции R связан с парными коэффициентами корреляции 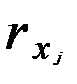соотношением

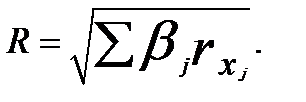(3.39)

Использование коэффициента множественной детерминации R2 для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину .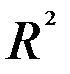

Поэтому при большом количестве факторов предпочтительнее использовать, так называемый, скорректированный, улучшенный (adjusted) коэффициент множественной детерминации 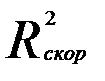, определяемый соотношением

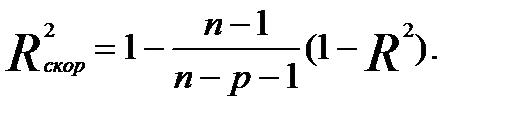(3.40)

Чем больше величина p, тем сильнее различия 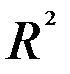и .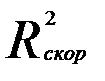

При использовании 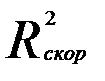для оценки целесообразности включения фактора в уравнение регрессии следует учитывать, что увеличение 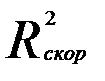при включении нового фактора не обязательно свидетельствует о его значимости, так как значение 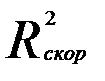увеличивается всегда, когда t - статистика по модулю больше единицы.

При заданном объеме наблюдений и при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации 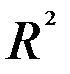имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Отметим, что низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации 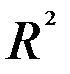может быть обусловлено следующими причинами:

– в регрессионную модель не включены существенные факторы;

– неверно выбрана форма аналитической зависимости, не отражающая реальные соотношения между переменными, включенными в модель.