Требования к факторам

Процесс отбора факторов в достаточно сложных ситуациях является итерационной процедурой, предполагающей, в частности, построение уравнений регрессии, и включает два этапа. Первоначально отбор факторов осуществляется на основе качественных соображений, исходя из представлений о природе взаимосвязи моделируемого показателя с другими экономическими показателями. На следующем этапе отобранные факторы подвергаются проверке на статистическую значимость. Окончательное решение о включении фактора в модель основывается на количественной оценке степени влияния фактора на изучаемый показатель.

К факторам, включаемым в модель, предъявляются следующие требования:

1. Факторы не должны быть взаимно коррелированы и, тем более, находиться в точной функциональной связи. Наличие высокой степени коррелированности между факторами может привести к неустойчивости и ненадежности оценок коэффициентов регрессии, а также к невозможности выделить изолированное влияние факторов на результативный показатель.

2. Включение фактора в модель должно приводить к существенному увеличению доли объясненной части в общей вариации зависимой переменной. Так как данная величина характеризуется таким показателем, как коэффициент детерминации 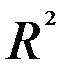, включение фактора в модель должно приводить к заметному изменению последнего. Формальная проверка существенности вклада фактора в модель выполняется с помощью оценки значимости соответствующего частного коэффициента корреляции либо значимости коэффициента в уравнении регрессии.

Если необходимо учесть влияние качественного фактора (не имеющего количественной оценки), то в модель включается соответствующая ему «фиктивная» переменная, имеющая конечное количество формально численных значений, соответствующих градациям качественного фактора. Например, если нужно учесть влияние уровня образования (на размер заработной платы), то в уравнение регрессии можно включить переменную z, принимающую значения z = 0 при начальном образовании, 1 -при среднем, 2 -при высшем.

Если для какого-либо показателя, который представляется важным для данного исследования, отсутствуют исходные данные, либо сам показатель четко не определен, то может быть полезно включить в модель некоторый ее «заменитель». Например, в качестве показателя качества образования можно использовать число преподавателей или расходы на одного студента. Такой подход основан на том факте, что не учет существенного показателя приводит к смещенным оценкам параметров. Например, производственная функция Кобба - Дугласа, построенная по данным экономики США за период 1949 – 1978 гг., построенная с учетом времени в качестве замещающей переменной для показателя технического прогресса имеет вид

logŶ = –1,03 + 0,17 logK + 0,93 logL + 0,024t,

(2,33) (0,66) (0,17) (0,016)

а без учета имеет вид

logŶ = –4,50+ 1,19 logK + 0,77 logL,

(0,57) (0,10) (0,15)

где 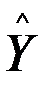–индекс объема выпуска частного сектора; K – индекс затрат капитала;

L –индекс затрат труда; t – время, равное единице в 1948 г. и т. д. Без учета замещающей переменной коэффициент при logK неправдоподобно велик.

При отборе факторов в модель следует, по возможности, стремиться к минимизации количества факторов, так как неоправданное их увеличение приводит к затруднениям в интерпретации модели и снижению достоверности результатов.