Мультиколлинеарность
Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.
При построении многофакторных моделей должно соблюдаться требование возможно меньшей коррелированности включенных в модель признаков-факторов (отсутствие мультиколлинеарности).
Мультиколлинеарность:
искажает величины параметров модели, которые имеют тенденцию к завышению;
приводит к изменению смысла экономической интерпретации коэффициентов регрессии;
вызывает слабую обусловленность системы нормальных уравнений;
осложняет процесс определения наиболее существенных факторных признаков.
В решении проблемы мультиколлинеарности можно выделить несколько этапов:
1. Установление наличия мультиколлинеарности:
а) проверяется выполнение условия:
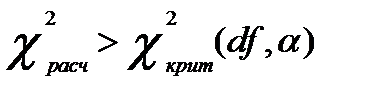 (3.5)
(3.5)
и вычисляется значение статистики Фаррара–Глоубера по следующей формуле:
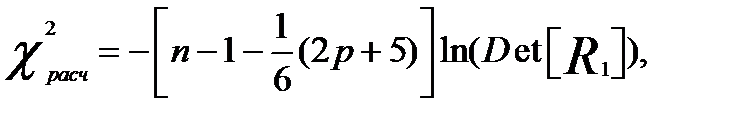 (3.6)
(3.6)
где 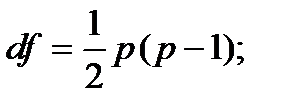
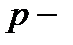 количество факторных признаков;
количество факторных признаков;
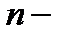 объём совокупности;
объём совокупности;
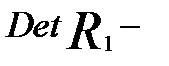 определитель матрицы парных межфакторных коэффициентов корреляции, которая получается вычёркиванием первой строки и первого столбца в табл. 3.1);
определитель матрицы парных межфакторных коэффициентов корреляции, которая получается вычёркиванием первой строки и первого столбца в табл. 3.1);
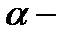 уровень значимости.
уровень значимости.
Критическое значение 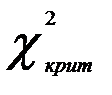 можно найти с помощью функции ХИ2.ОБР.ПХ
можно найти с помощью функции ХИ2.ОБР.ПХ
Если условие (3.5) выполняется, то это означает, что  недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной;
недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной;
б) высокие значения парных линейных межфакторных коэффициентов корреляции указывают на наличие интеркорреляции, т.е. линейной связи между двумя объясняющими переменными. Чем выше величина 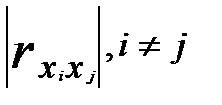 , тем выше интеркорреляция. Факторы
, тем выше интеркорреляция. Факторы 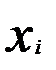 и
и 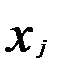 могут быть признаны коллинеарными, если
могут быть признаны коллинеарными, если 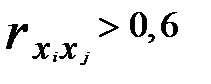 то это свидетельствует о наличии интеркорреляции;
то это свидетельствует о наличии интеркорреляции;
в) если 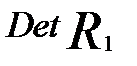 близок к нулю, то это свидетельствует о наличии мультиколлинеарности.
близок к нулю, то это свидетельствует о наличии мультиколлинеарности.
Таблица 3.2
Матрица парных коэффициентов корреляции
| Признак | 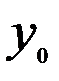
| 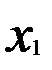
| 
| 
| 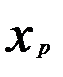
|
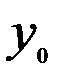
| 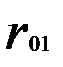
| 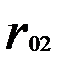
| 
| 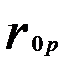
| |
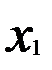
| 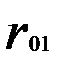
| 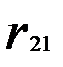
| 
| 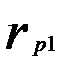
| |

| 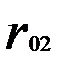
| 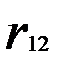
| 
| 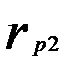
| |

| 
| 
| 
| 
| 
|
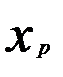
| 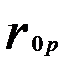
| 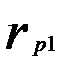
| 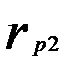
| 
|
2. Определение причин возникновения мультиколлинеарности:
а) изучаемые факторные признаки характеризуют одну и ту же сторону явления или процесса (например, показатели объема произведенной продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как оба характеризуют размер предприятия).
б) использование в качестве факторных признаков, суммарное значение которых представляет собой постоянную величину (например, коэффициент годности и коэффициент износа основных фондов)
в) факторные признаки, являющиеся элементами друг друга (например, затраты на производство продукции и себестоимость единицы продукции)
г) факторные признаки, по экономическому смыслу дублирующие друг друга (например, прибыль и рентабельность продукции)
3. Разработка мер по устранению мультиколлинеарности
Устранение мультиколлинеарности возможно посредством исключения из корреляционной модели одного или нескольких линейно связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы. Вопрос о том, какой из факторов следует отбросить, решается на основе качественного и логического анализа изучаемого явления.
Методы устранения или уменьшения мультиколлинеарности:
Сравнение значений линейных межфакторных коэффицентов корреляции:
Суть метода: выбирается наибольшее абсолютное значение среди линейных межфакторных коэффициентов корреляции. Предпочтение отдается тому фактору, который более тесно, чем другие факторы, связан с результативным признаком, причем желательно, чтобы связь данного факторного признака с y была больше, чем его связь с другим факторным признаком, т.е.
 (3.7)
(3.7)
Далее снова проверяется выполнение условия (3.3) и так далее до тех пор, пока не будет исключена мультиколлинеарность.
Метод исключения факторов на основе частных коэффициентов корелляции и детерминации
Частные коэффициенты корреляции, позволяют установить степень тесноты связи между результативным признаком у и каждым из факторных признаков при исключении искажающего влияния других факторных признаков. Следовательно, коэффициенты частной корреляции отражают степень «чистого» влияния факторного признака на результативный признак. Для их расчета могут быть использованы парные коэффициенты корреляции.
Для случая зависимости результативного признака у от двух признаков-факторов ( 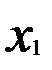 и
и  ) определяются два коэффициента частной корреляции:
) определяются два коэффициента частной корреляции:
• частный коэффициент корреляции между результативным признаком у и фактором 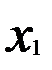 при элиминировании фактора
при элиминировании фактора 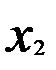 :
:
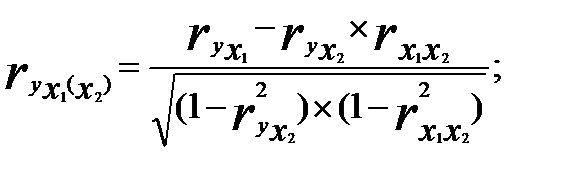 (3.8)
(3.8)
• частный коэффициент корреляции между результативным признаком у и фактором 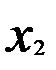 при элиминировании фактора
при элиминировании фактора 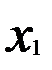 :
:
 (3.9)
(3.9)
Для общего случая частные коэффициенты корреляции определяются по формуле
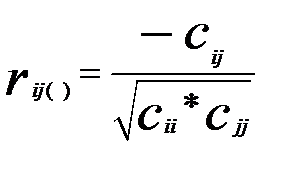 (3.10)
(3.10)
где  — обратная матрица матрицы
— обратная матрица матрицы 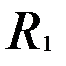 .
.
Величина частного коэффициента корреляции лежит в пределах от 0 до 1, а знак определяется знаком соответствующих параметров регрессии.
Рассчитывая величины частных коэффициентов корреляции, следует иметь в виду, что каждый из них по своей абсолютной величине не может быть больше величины коэффициента множественной (совокупной) корреляции 
Частные коэффициенты детерминации позволяют оценить вклад в мультиколлинеарность каждого из факторных признаков и вычисляются по формуле
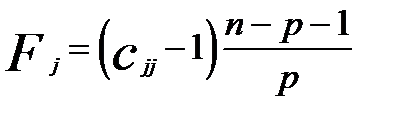 (3.11)
(3.11)
Фактические значения F-критерия сравниваются с критическими, вычисляемыми для степеней свободы 
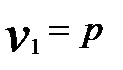 ,
, 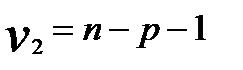 и уровне значимости
и уровне значимости  . Если
. Если 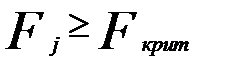 то соответствующие независимые переменные мультиколлениарны с другими.
то соответствующие независимые переменные мультиколлениарны с другими.
Далее осуществляется проверка наличия интеркорреляции каждой пары переменных. С этой целью по выражению (3.10) вычисляются частные коэффициенты корреляции и значения t-критериев Стъюдента по формуле
 (3.12)
(3.12)
Фактические значения t-критериев сравниваются с критическими при степенях свободы 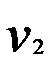 и уровне значимости
и уровне значимости  .Если
.Если 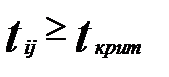 то между соответствующими независимыми переменные присутствует интеркорреляция. Удалить следует ту переменную, у которой большее значение F-критерия.
то между соответствующими независимыми переменные присутствует интеркорреляция. Удалить следует ту переменную, у которой большее значение F-критерия.
Далее снова проверяется выполнение условия (3.5) и так далее до тех пор, пока не будет исключена мультиколлинеарность.
Метод главных компонент
Если по каким-то причинам перечень независимых переменных не подлежит изменению, то с целью исключения мультиколинеарности можно воспользоваться методом главных компонент.
Применение метода главных компонент предполагает переход от взаимозависимых переменных х к независимым друг от друга переменным z, которые называют главными компонентами. Каждая главная компонента  может быть представлена как линейная комбинация стандартизованных объясняющих переменных
может быть представлена как линейная комбинация стандартизованных объясняющих переменных 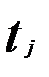 , которые определяются по формуле:
, которые определяются по формуле:
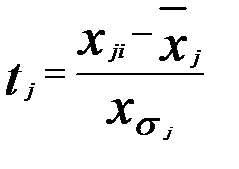 . (3.13)
. (3.13)
Количество компонент может быть меньше или равно количеству исходных независимых переменных р. Компоненту с номером k можно записать следующим образом:
 . (3.14)
. (3.14)
Оценки 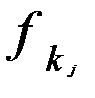 в формуле (3.14) соответствуют элементам k-го собственного вектора матрицы
в формуле (3.14) соответствуют элементам k-го собственного вектора матрицы 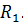
Нумерация главных компонент не является произвольной. Первая главная компонента имеет максимальную дисперсию, ей соответствует максимальное собственное число матрицы 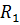 , последняя — минимальную дисперсию и наименьшее собственное число.
, последняя — минимальную дисперсию и наименьшее собственное число.
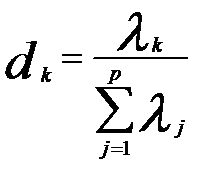 (3.15)
(3.15)
где  — собственное число, соответствующее данной компоненте; в знаменателе формулы (3) приведена сумма всех собственных чисел матрицы
— собственное число, соответствующее данной компоненте; в знаменателе формулы (3) приведена сумма всех собственных чисел матрицы 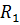 .
.
После расчета значений компонент 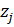 строят регрессию, используя МНК.
строят регрессию, используя МНК.
 , (3.16)
, (3.16)
гдеty— стандартизованная зависимая переменная; 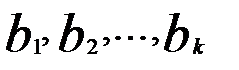 —коэффициенты регрессии по главным компонентам; z1,z2,...,zk—главные компоненты, упорядоченные по убыванию собственных чисел
—коэффициенты регрессии по главным компонентам; z1,z2,...,zk—главные компоненты, упорядоченные по убыванию собственных чисел  ;
;  — случайный остаток.
— случайный остаток.
После оценки параметров регрессии (3.14) можно перейти к уравнению регрессии в исходных переменных, используя выражения (3.14)—(3.15).
Рассмотрим применение перечисленных методов на данных примера 1
Пример 1.По данным, полученным от 40 промышленных предприятий одного из регионов, изучается зависимость объема выпуска продукции Y(млн. руб.) от четырех факторов:
X1 - численность промышленно-производственного персонала, чел.;
X2- среднегодовая стоимость основных фондов, млн руб.;
X3- электровооруженность 1 чел.-ч., кВт-ч;
X4- прибыль от реализации продукции, млн руб.
| № | Y | X1 | X2 | X3 | X4 |
| 62 240 | 2 890 | 30 434 | 13,9 | 1 258 | |
| 88 569 | 4 409 | 162 229 | 55,3 | 16 304 | |
| 3 118 | 2 370 | 5,7 | |||
| 186 256 | 5 436 | 802 725 | 87,2 | 8 306 | |
| 56 262 | 1 559 | 48 075 | 56,2 | 17 663 | |
| 19 216 | 18 894 | 27,6 | 2 861 | ||
| 16 567 | 1 197 | 19 621 | 31,1 | ||
| 203 456 | 8 212 | 336 472 | 60,5 | 42 392 | |
| 13 425 | 9 843 | 33,5 | 4 740 | ||
| 31 163 | 1 405 | 44 217 | 35,1 | 9 469 | |
| 30 109 | 1 575 | 34 142 | 26,5 | 5 206 | |
| 14 781 | 6 412 | 4,4 | -1 437 | ||
| 41 138 | 1 866 | 39 208 | 24,9 | 9 948 | |
| 69 202 | 4 419 | 80 694 | 13,2 | -9 135 | |
| 10 201 | 6 714 | 14,9 | |||
| 75 282 | 2 600 | 28 148 | 2,4 | 12 729 | |
| 47 064 | 1 110 | 11 861 | 5,8 | 8 887 | |
| 57 342 | 1 147 | 63 273 | 50,4 | 15 503 | |
| 32 900 | 16 144 | 4,9 | 7 960 | ||
| 18 135 | 14 758 | 25,9 | 2 522 | ||
| 29 589 | 1 003 | 27 642 | 43,5 | 4 412 | |
| 22 604 | 1 680 | 23 968 | 3,1 | 3 304 | |
| 1 878 | 0,6 | ||||
| 49 378 | 2 505 | 85 105 | 43,1 | 6 264 | |
| 6 896 | 1 556 | 12 612 | 0,7 | 1 745 | |
| 3 190 | 0,2 | ||||
| 5 384 | 3 667 | 6,6 | 1 225 | ||
| 17 668 | 16 250 | 4,8 | 4 652 | ||
| 24 119 | 1 142 | 28 266 | 48,7 | 5 278 | |
| 16 649 | 8 228 | 17,8 | 5 431 | ||
| 6 925 | 1 481 | 3,0 | 2 213 | ||
| 5 394 | 3 797 | 20,8 | 1 454 | ||
| 4 330 | 2 950 | 23,9 | 1 764 | ||
| 1 087 322 | 46 142 | 972 349 | 27,5 | 163 420 | |
| 284 154 | 10 469 | 272 622 | 33,2 | 27 506 | |
| 363 204 | 16 063 | 267 652 | 23,1 | 72 782 | |
| 162 216 | 6 139 | 128 731 | 35,1 | 35 218 | |
| 97 070 | 4 560 | 108 549 | 32,5 | 10 035 | |
| 55 410 | 2 797 | 60 209 | 37,2 | 1 021 | |
| 32 654 | 1 922 | 60 669 | 33,8 | 5 192 |
Сравнение значений линейных межфакторных коэффицентов корреляции:
| Y | X1 | X2 | X3 | X4 | ||
| Y | 1,000 | 0,996 | 0,854 | 0,190 | 0,968 | |
| R= | X1 | 0,996 | 1,000 | 0,826 | 0,149 | 0,966 |
| X2 | 0,854 | 0,826 | 1,000 | 0,480 | 0,770 | |
| X3 | 0,190 | 0,149 | 0,480 | 1,000 | 0,174 | |
| X4 | 0,968 | 0,966 | 0,770 | 0,174 | 1,000 |
| X1 | X2 | X3 | X4 | ||
| X1 | 1,000 | 0,826 | 0,149 | 0,966 | |
| R1= | X2 | 0,826 | 1,000 | 0,480 | 0,770 |
| X3 | 0,149 | 0,480 | 1,000 | 0,174 | |
| X4 | 0,966 | 0,770 | 0,174 | 1,000 |
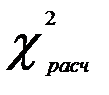 =167,01;
=167,01; 
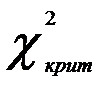 =12,59. Условие (3.5) выполняется, следовательно мультиколлинеарность присутствует.
=12,59. Условие (3.5) выполняется, следовательно мультиколлинеарность присутствует.
В соответствии (3.7) исключаем фактор 4.
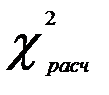 =62,97;
=62,97; 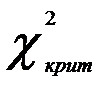 =7,81.
=7,81.
Исключаем фактор 2.
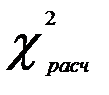 =0,84;
=0,84; 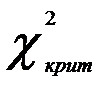 =3,84. Условие (3.5) не выполняется, следовательно мультиколлинеарность отсутствует.
=3,84. Условие (3.5) не выполняется, следовательно мультиколлинеарность отсутствует.
Определим параметры уравнения регрессии с помощью режима “Регрессия”
Как следует из итогов параметры уравнения и уравнение в целом значимы.
Точность (величина ошибки) 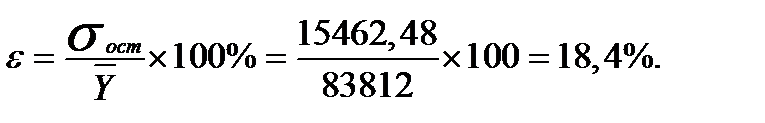
Метод исключения факторов на основе частных коэффициентов корреляции и детерминации
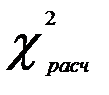 =167,01;
=167,01; 
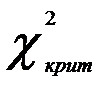 =12,59. Условие (3.5) выполняется, следовательно, мультиколлинеарность присутствует.
=12,59. Условие (3.5) выполняется, следовательно, мультиколлинеарность присутствует.
| X1 | X2 | X3 | X4 | ||
| X1 | 25,66 | -8,06 | 3,40 | -19,17 | |
| C= | X2 | -8,06 | 6,05 | -2,32 | 3,53 |
| X3 | 3,40 | -2,32 | 1,93 | -1,83 | |
| X4 | -19,17 | 3,53 | -1,83 | 17,11 |
| F1 | F2 | F3 | F4 | Fкрит |
| 215,8 | 44,2 | 8,1 | 141,0 | 2,6 |
Все частные коэффициенты детерминации больше их критического значения, что подтверждает ранее сделанный вывод о наличии мультиколлинеарности.
| rij | tij | tkr | |
| 0,647 | 5,02 | 2,03 | |
| -0,483 | -3,26 | ||
| 0,915 | 13,39 | ||
| 0,680 | 5,48 | ||
| -0,347 | -2,19 | ||
| 0,319 | 1,99 |
Все расчётные значения t-критерия, кроме 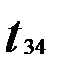 ,больше критического. Максимальное значение между первым и четвёртым факторами. Для того чтобы избавиться от интеркорреляции необходимо исключить фактор
,больше критического. Максимальное значение между первым и четвёртым факторами. Для того чтобы избавиться от интеркорреляции необходимо исключить фактор 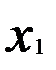 так как у него большее значение F-критерия. Следовательно, он больше влияет на общую мультиколлинеарность факторов.
так как у него большее значение F-критерия. Следовательно, он больше влияет на общую мультиколлинеарность факторов.
Далее в процессе решения был исключён фактор 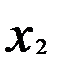 . Матрица
. Матрица 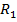 имеет следующий вид
имеет следующий вид
| X3 | X4 | ||
 = =
| X3 | 1,000 | 0,174 |
| X4 | 0,174 | 1,000 |
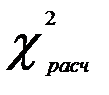 =1,16;
=1,16; 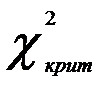 =3,84. Условие (3.5) не выполняется, следовательно мультиколлинеарность отсутствует.
=3,84. Условие (3.5) не выполняется, следовательно мультиколлинеарность отсутствует.
Определим параметры уравнения регрессии с помощью режима “Регрессия”
В связи с тем, что параметр 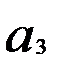 не значим,
не значим, 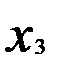 фактор 3 исключим из дальнейшего рассмотрения.
фактор 3 исключим из дальнейшего рассмотрения.
Как следует из итогов параметры уравнения и уравнение в целом значимы.
Точность (величина ошибки) 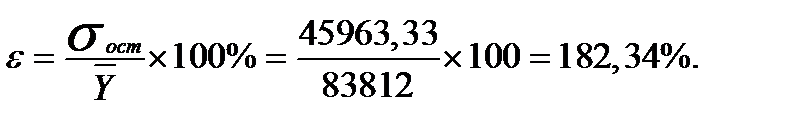
Рассмотрим вариант короткой регрессии (первый метод без учёта третьего фактора
Как следует из итогов параметры уравнения и уравнение в целом значимы.
Точность (величина ошибки) 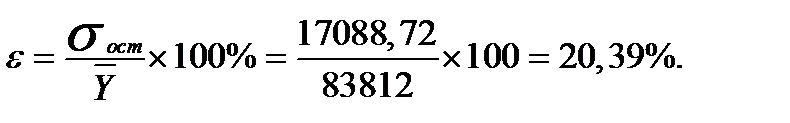
Целесообразность включения фактора Х3 рассмотрим с помощью теста на выбор «длинной» и «короткой» регрессии. Этот тестиспользуется для отбора наиболее существенных объясняющих переменных. Иногда переход от большего числа исходных показателей анализируемой системы к меньшему числу наиболее информативных факторов может быть объяснен дублированием информации из-за сильно взаимосвязанных факторов. Стремление к построению более простой модели приводит к идее уменьшения размерности модели без потери ее качества. Для этого используют тестпроверки “длинной” и “короткой” регрессий.
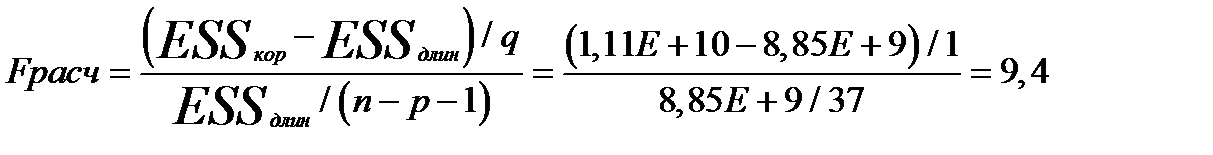
Если 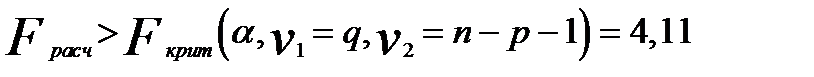 , то гипотеза отвергается (выбираем “длинную”регрессию).
, то гипотеза отвергается (выбираем “длинную”регрессию).
Метод главных компонент
Обратимся к программе STATISTICA 6.1.по следующей схеме: Анализ→Многомерный разведочный анализ→Анализ главных компонент и классификация. Введём массив исходных данных примера 1.Результатом решения являются собственные числа и собственные векторы матрицы 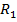 .
.
| 
| 
| 
|
| 2,825 | 0,984 | 0,1677 | 0,023 |
| Собственные векторы | ||||
| Фактор 1 | Фактор 2 | Фактор 3 | Фактор 4 | |
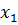
| -0,566 | -0,282 | -0,124 | 0,764 |
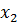
| -0,556 | 0,154 | 0,785 | -0,227 |
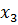
| -0,245 | 0,909 | -0,322 | 0,102 |
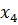
| -0,557 | -0,267 | -0,515 | -0,595 |
| Номер фактора | Собственные числа | Процент общей дисперсии | Кумулятивные значения собственных чисел | Кумулятивный процент общей дисперсии | |
| 2,825 | 70,635 | 2,825 | 70,635 | ||
| 0,984 | 24,597 | 3,809 | 95,232 | ||
| 0,168 | 4,192 | 3,977 | 99,424 | ||
| 0,023 | 0,576 | 4,000 | 100,000 |
Рис. 3. Процент общей дисперсии собственныхчисел матрицы корреляции
| 0,826 | 0,149 | 0,966 | ||
| R1= | 0,826 | 0,48 | 0,77 | |
| 0,149 | 0,48 | 0,174 | ||
| 0,966 | 0,77 | 0,174 |
Матрица парных линейных коэффициентов корреляции между независимыми переменными примера 1.
Собственные числа на рис.3 представлены в порядке убывания, отражая тем самым степень важности соответствующих факторов для объяснения вариации исходных данных. Так фактор, соответствующий максимальному собственному числу (2,825), описывает 70,635% общей вариации. Второй фактор для значения (0,984) описывает 24,597% общей вариации и т.д.
На практике применяют различные критерии для правильного выбора факторного пространства. Наиболее простой из них – оставить только те факторы, собственные числа которых больше 1. В данном примере только первое собственное число больше 1, т.е. можно оставить в факторном пространстве первый фактор. Вместе с тем оставим первые два фактора. С этой целью сформируем массив стандартизованных переменных по формуле (3.13)
| ty | t1 | t2 | t3 | t4 |
| -0,121 | -0,088 | -0,334 | -0,586 | -0,412 |
| 0,027 | 0,115 | 0,332 | 1,511 | 0,127 |
| -0,452 | -0,445 | -0,476 | -1,001 | -0,448 |
| 0,574 | 0,252 | 3,566 | 3,126 | -0,160 |
| -0,154 | -0,265 | -0,245 | 1,556 | 0,176 |
| -0,362 | -0,348 | -0,392 | 0,108 | -0,355 |
| -0,377 | -0,314 | -0,388 | 0,285 | -0,431 |
| 0,671 | 0,622 | 1,212 | 1,774 | 1,063 |
| -0,395 | -0,412 | -0,438 | 0,407 | -0,287 |
| -0,295 | -0,286 | -0,264 | 0,488 | -0,118 |
| -0,301 | -0,263 | -0,315 | 0,052 | -0,271 |
| -0,387 | -0,345 | -0,455 | -1,067 | -0,509 |
| -0,239 | -0,224 | -0,290 | -0,029 | -0,101 |
| -0,082 | 0,116 | -0,080 | -0,621 | -0,785 |
| -0,413 | -0,366 | -0,454 | -0,535 | -0,427 |
| -0,048 | -0,126 | -0,345 | -1,168 | -0,001 |
| -0,206 | -0,325 | -0,428 | -0,996 | -0,139 |
| -0,148 | -0,320 | -0,168 | 1,263 | 0,099 |
| -0,285 | -0,358 | -0,406 | -1,041 | -0,172 |
| -0,368 | -0,371 | -0,413 | 0,022 | -0,367 |
| -0,304 | -0,339 | -0,348 | 0,913 | -0,299 |
| -0,343 | -0,249 | -0,366 | -1,133 | -0,339 |
| -0,459 | -0,463 | -0,486 | -1,259 | -0,451 |
| -0,193 | -0,139 | -0,058 | 0,893 | -0,233 |
| -0,431 | -0,266 | -0,424 | -1,254 | -0,395 |
| -0,452 | -0,414 | -0,485 | -1,279 | -0,453 |
| -0,440 | -0,433 | -0,469 | -0,955 | -0,413 |
| -0,371 | -0,357 | -0,405 | -1,046 | -0,291 |
| -0,335 | -0,321 | -0,345 | 1,177 | -0,268 |
| -0,377 | -0,379 | -0,446 | -0,388 | -0,263 |
| -0,431 | -0,452 | -0,480 | -1,138 | -0,378 |
| -0,440 | -0,429 | -0,468 | -0,236 | -0,405 |
| -0,446 | -0,444 | -0,473 | -0,079 | -0,394 |
| 5,627 | 5,681 | 4,422 | 0,103 | 5,402 |
| 1,123 | 0,923 | 0,889 | 0,392 | 0,529 |
| 1,567 | 1,669 | 0,864 | -0,120 | 2,152 |
| 0,440 | 0,346 | 0,163 | 0,488 | 0,805 |
| 0,074 | 0,135 | 0,061 | 0,356 | -0,098 |
| 0,159 | -0,100 | -0,183 | 0,594 | -0,421 |
| -0,287 | -0,217 | -0,181 | 0,422 | -0,271 |
Введём обозначения матрицы собственных векторов
| -0,566 | -0,282 | -0,124 | 0,764 | |
| F= | -0,556 | 0,154 | 0,785 | -0,227 |
| -0,245 | 0,909 | -0,322 | 0,102 | |
| -0,557 | -0,267 | -0,515 | -0,595 |
Четыре компоненты, соответствующие четырём собственным векторам, можно записать в следующем виде
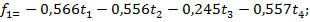
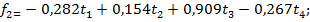
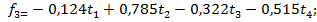
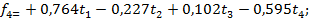
Умножим матрицу стандартизованных независимых переменных (Т) на матрицу F.
Результатом умножения является матрица Z.
| ty | z1 | z2 | z3 | z4 |
| -0,121 | 0,609 | -0,449 | 0,150 | 0,194 |
| 0,027 | -0,691 | 1,357 | -0,306 | 0,090 |
| -0,452 | 1,012 | -0,737 | 0,235 | -0,067 |
| 0,574 | -2,802 | 3,360 | 1,842 | -0,206 |
| -0,154 | -0,194 | 1,405 | -0,751 | -0,094 |
| -0,362 | 0,586 | 0,231 | -0,117 | 0,045 |
| -0,377 | 0,564 | 0,403 | -0,136 | 0,134 |
| 0,671 | -2,053 | 1,339 | -0,245 | -0,252 |
| -0,395 | 0,537 | 0,495 | -0,276 | -0,003 |
| -0,295 | 0,255 | 0,515 | -0,269 | -0,039 |
| -0,301 | 0,462 | 0,146 | -0,092 | 0,037 |
| -0,387 | 0,993 | -0,806 | 0,291 | 0,034 |
| -0,239 | 0,351 | 0,020 | -0,138 | -0,049 |
| -0,082 | 0,569 | -0,400 | 0,527 | 0,511 |
| -0,413 | 0,828 | -0,339 | 0,081 | 0,022 |
| -0,048 | 0,551 | -1,078 | 0,122 | -0,136 |
| -0,206 | 0,743 | -0,842 | 0,097 | -0,170 |
| -0,148 | -0,090 | 1,186 | -0,550 | -0,137 |
| -0,285 | 0,780 | -0,862 | 0,150 | -0,185 |
| -0,368 | 0,639 | 0,159 | -0,096 | 0,030 |
| -0,304 | 0,328 | 0,952 | -0,371 | 0,090 |
| -0,343 | 0,811 | -0,925 | 0,283 | -0,021 |
| -0,459 | 1,093 | -0,968 | 0,314 | -0,103 |
| -0,193 | 0,021 | 0,904 | -0,196 | 0,136 |
| -0,431 | 0,914 | -1,024 | 0,308 | 0,001 |
| -0,452 | 1,071 | -0,999 | 0,316 | -0,067 |
| -0,440 | 0,970 | -0,708 | 0,206 | -0,075 |
| -0,371 | 0,846 | -0,835 | 0,213 | -0,114 |
| -0,335 | 0,234 | 1,178 | -0,472 | 0,112 |
| -0,377 | 0,704 | -0,244 | -0,043 | -0,071 |
| -0,431 | 1,012 | -0,879 | 0,241 | -0,127 |
| -0,440 | 0,787 | -0,058 | -0,030 | -0,005 |
| -0,446 | 0,753 | 0,086 | -0,087 | -0,006 |
| 5,627 | -8,709 | -2,270 | -0,047 | 0,136 |
| 1,123 | -1,407 | 0,091 | 0,185 | 0,229 |
| 1,567 | -2,595 | -1,021 | -0,598 | -0,212 |
| 0,440 | -0,855 | 0,156 | -0,487 | -0,202 |
| 0,074 | -0,143 | 0,321 | -0,034 | 0,184 |
| -0,159 | 0,247 | 0,652 | -0,107 | 0,276 |
| -0,287 | 0,271 | 0,489 | -0,112 | 0,079 |
Полученные данные обработаем с помощью режима “Регрессия”
В полученном уравнении регрессии значимы параметры по всем четырём компонентам.
Далее будем рассматривать только первые два фактора, так как они описывают более 95% общей вариации результативного признака.
В соответствии с формулой
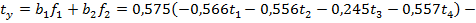
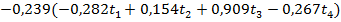 .
.
После приведения подобных членов имеем следующее уравнение регрессии
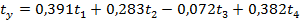
Преобразуем полученное выражение в регрессию с исходными переменными:
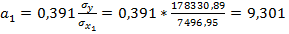 и т.д.
и т.д.
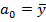 -
- 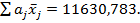
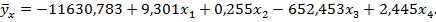
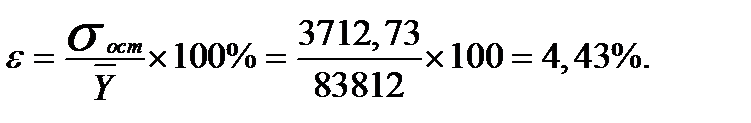
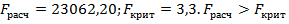 следовательно, выбираем регрессию с 2-мя факторами.
следовательно, выбираем регрессию с 2-мя факторами.
Таким образом, метод главных компонент позволил получить наилучший результат.
Метод включения факторов (метод пошаговой регрессии).
Суть метода заключается в том, что в модель включаются факторы по одному в определенной последовательности. На первом шаге в модель вводится тот фактор, который имеет наибольший коэффициент корреляции с зависимой переменной.
На втором и последующих шагах в модель включается фактор, который имеет наибольший коэффициент корреляции с остатками модели.
После включения каждого фактора в модель рассчитываются ее характеристики и модель проверяют на достоверность.
Построение модели заканчивается, если модель перестает удовлетворять определенным условиям (например, 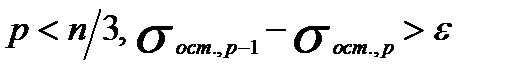 , где n –число наблюдений;
, где n –число наблюдений; 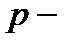 число факторных признаков, включаемых в модель;
число факторных признаков, включаемых в модель; 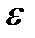 –некоторое заданное малое число;
–некоторое заданное малое число; 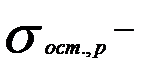 остаточное среднеквадратическое отклонение;
остаточное среднеквадратическое отклонение; 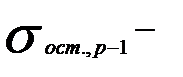 остаточное среднеквадратическое отклонение, полученное на предыдущем шаге и включающее
остаточное среднеквадратическое отклонение, полученное на предыдущем шаге и включающее 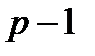 переменных).
переменных).
Метод исключения факторов.
Применяется после устранения мультиколлинеарности. Суть метода состоит в том, что в модель включаются все факторы. Затем после построения уравнения регрессии из модели исключают фактор, коэффициент при котором незначим и имеет наименьшее значение t- критерия. После этого получают новое уравнение регрессии и снова проводят оценку значимости всех оставшихся коэффициентов регрессии.
Процесс исключения факторов продолжается до тех пор, пока модель не станет удовлетворять определенным условиям и все коэффициенты регрессии не будут значимы.
Отобранные факторы включаются в модель множественной зависимости. При этом следует учитывать, что число факторов, включаемых в модель, должно быть в 7 — 8 раз меньше, чем число единиц, входящих в совокупность.
Дата добавления: 2016-03-22; просмотров: 2146;
