Этапы эконометрического моделирования
1. Постановочный. Формулируется цель исследования (анализ, прогноз, управленческое решение), определяются экономические переменные модели).
2. Априорный. Анализируется изучаемое явление, формируется и формализуется информация известная до начала исследования.
3. Параметризация.Определяется вид модели, выражается в математической форме взаимосвязь между её переменными, формулируются исходные предпосылки и ограничения модели.
4. Информационный. Собирается необходимая статистическая информация.
5. Идентификация модели. Проводится статистический анализ модели, оценивается точность, значимость её параметров и модели в целом.
6. Верификация модели. Оцениваем адекватность модели, т.е. соответствие реальному экономическому процессу.
Лекция №2
Модели парной регрессии
Построение уравнения парной регрессии
Уравнение адекватно реальному моделируемому явлению или процессу в случае соблюдения следующих требований:
- cовокупность исходных данных должна быть однородной и математически описываться непрерывными функциями;
- наличие достаточно большого объема исследуемой выборочной совокупности;
- возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей;
- причинно-следственные связи между явлениями и процессами, по возможности, следует описывать линейной (или приводимой к линейной) формой зависимости;
- отсутствие количественных ограничений на параметры модели
- количественное выражение факторных признаков;
- постоянство территориальной и временной структуры изучаемой совокупности.
Теоретическая обоснованность моделей взаимосвязи явлений обеспечивается соблюдением определенных условий:
- все признаки и их совместные распределения должны подчиняться нормальному закону распределения;
- дисперсия моделируемого признака должна всё время оставаться постоянной при изменении значений факторного признака;
- отдельные наблюдения должны быть независимы, т.е. результаты, полученные в iнаблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а также влиять на них.
При линейной связи параметры ( 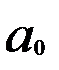 и
и 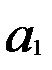 ) уравнения парной регрессии:
) уравнения парной регрессии:
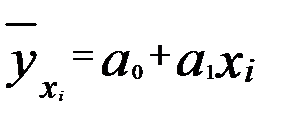 (2.1)
(2.1)
находятся с помощью метода наименьших квадратов. Суть метода заключается в минимизации суммы квадратов отклонений теоретических значений результативного признака ( 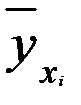 ) от его фактических значений (
) от его фактических значений ( 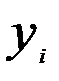 ):
):
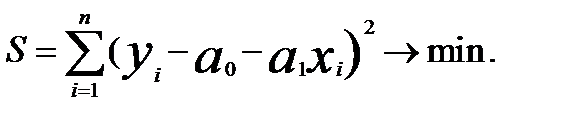 (2.2)
(2.2)
Условие (2.2) выполняется при равенстве нулю частных производных по параметрам 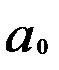 и
и 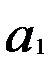 :
:
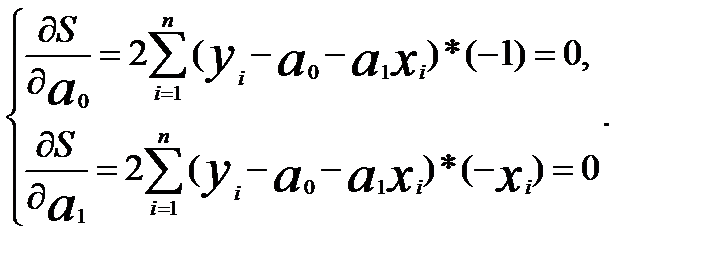 (2.3)
(2.3)
Сократим каждое уравнение системы (2.3) на (-2), раскроем скобки и получим следующую систему нормальных уравнений:
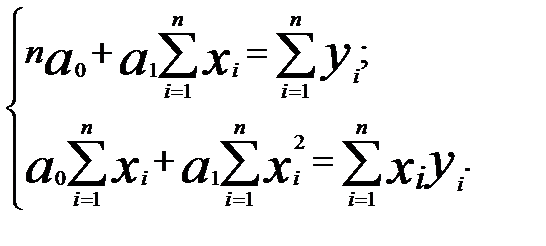 (2.4)
(2.4)
Поделим каждое уравнение системы (2.4) на объём статистической совокупности (n), тогда упомянутую систему можно представить в более наглядном виде:
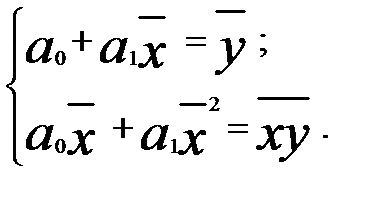 (2.5)
(2.5)
Из первого уравнения системы (1,5) следует, что:
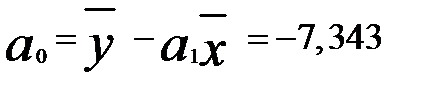 (2.6) Подставив полученное выражение во второе уравнение, получим:
(2.6) Подставив полученное выражение во второе уравнение, получим:
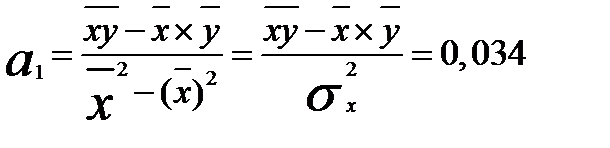 . (2.7) Коэффициент корреляции определяется по формуле:
. (2.7) Коэффициент корреляции определяется по формуле:
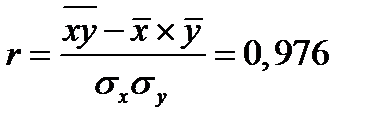 (2.8) Учитывая (1,7) и (1,8) получим
(2.8) Учитывая (1,7) и (1,8) получим
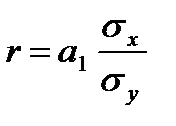 (2.9)
(2.9)
или 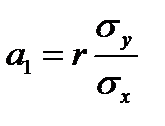 . (2.10)
. (2.10)
Зная значения r, 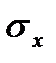 и
и 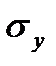 можно вычислить по выражениям (2.10) и (2.6) параметры
можно вычислить по выражениям (2.10) и (2.6) параметры 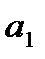 и
и 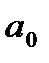 линейного уравнения регрессии.
линейного уравнения регрессии.
Параметр 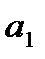 , нельзя использовать для непосредственной оценки влияния факторного признака на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляют значение среднего коэффициента эластичности и бета-коэффициент:
, нельзя использовать для непосредственной оценки влияния факторного признака на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляют значение среднего коэффициента эластичности и бета-коэффициент:
 (2.11)
(2.11)
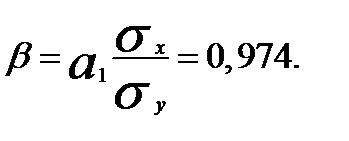 (2.12)
(2.12)
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака x на один процент.
Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину своего среднего квадратического отклонения.
Статистический анализ модели
Оценка параметров парной регрессии выполняется исходя из следующих предпосылок. Допустим, что в генеральной совокупности связь между x и y линейна. Наличие случайных отклонений, вызванных воздействием на переменную y множества других, неучтенных в уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин 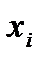 и
и 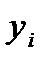 приобретает вид:
приобретает вид:
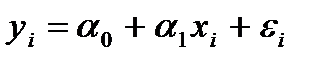
Здесь 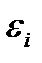 - случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений
- случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений 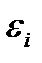 , то можно было бы рассчитать значения параметров
, то можно было бы рассчитать значения параметров 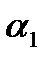 и
и  . Так как они неизвестны, то по наблюдениям
. Так как они неизвестны, то по наблюдениям 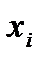 и
и 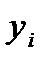 можно получить только оценки параметров
можно получить только оценки параметров 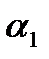 и
и 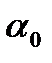 , которые сами являются случайными величинами в связи с тем, что соответствуют случайной выборке. Пусть
, которые сами являются случайными величинами в связи с тем, что соответствуют случайной выборке. Пусть 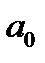 - оценка параметра
- оценка параметра 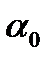 ,
, 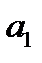 - оценка параметра
- оценка параметра 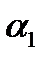 , тогда оцененное уравнение регрессии будет иметь вид:
, тогда оцененное уравнение регрессии будет иметь вид:
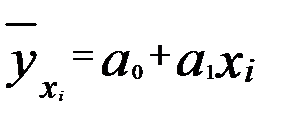 (2.13)
(2.13)
Для того чтобы оценки 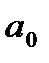 и
и 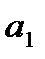 обладали адекватностью ряд остатков
обладали адекватностью ряд остатков
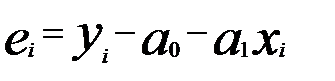 должен удовлетворять следующим требованиям:
должен удовлетворять следующим требованиям:
- математическое ожидание 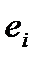 равно нулю (критерий нулевого среднего);
равно нулю (критерий нулевого среднего);
- величина 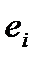 является случайной переменной (критерий серий);
является случайной переменной (критерий серий);
- значения 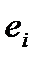 независимы между собой (критерий Дарбина-Уотсона);
независимы между собой (критерий Дарбина-Уотсона);
- дисперсия 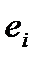 постоянна:
постоянна: 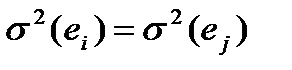 для всех i, j (тест Гольдфельда-Квандта);
для всех i, j (тест Гольдфельда-Квандта);
- остатки распределены по нормальному закону (свойство используется для проверки статистической значимости и построения доверительных интервалов при прогнозировании).
Известно, что если данные условия выполняются, то оценки, сделанные с помощью метода наименьших квадратов, обладают следующими свойствами:
- оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению:
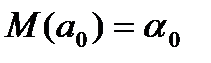
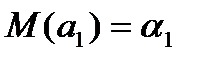
Это вытекает из того, что 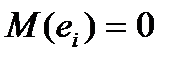 и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;
и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;
- оценки состоятельны, т.к. дисперсии оценок параметров при возрастании числа наблюдений стремятся к нулю: 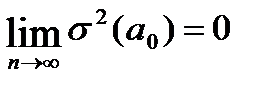 ;
; 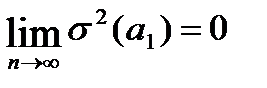 т.е. надежность оценки при увеличении выборки растёт;
т.е. надежность оценки при увеличении выборки растёт;
- оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра.
Если предположения 3 и 4 нарушены, т.е. дисперсия возмущений непостоянна или значения  связаны друг с другом, то свойства несмещености и состоятельности сохраняется, но свойства эффективности – нет.
связаны друг с другом, то свойства несмещености и состоятельности сохраняется, но свойства эффективности – нет.
Отметим, что аппроксимировать уравнением парной регрессии у на х, имеет смысл только в том случае, если существует достаточно тесная статистическая зависимость между случайными величинами и линейный коэффициент корреляции является значимым, что и имеет место в рассматриваемом примере.
Оценка качества построенной модели
Таблица 1.1
| |
Формально качество модели определяется ее адекватностью и точностью. Эти свойства исследуются на основе анализа ряда остатков, значения которых вычислены по выражению  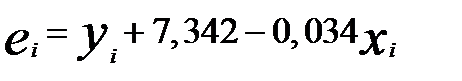 .
Табл.1.1 содержит: .
Табл.1.1 содержит: 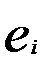 - остатки для задачи, исходные данные которой приведены в табл. 5.2; - остатки для задачи, исходные данные которой приведены в табл. 5.2; 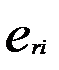 - ранжированные значения ряда остатков; - ранжированные значения ряда остатков; 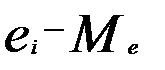 - остатки за вычетом медианы остатков; - остатки за вычетом медианы остатков; 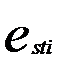 - стандартные остатки.
Адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так какнекоторые из них используются прирасчете различных критериев адекватности. - стандартные остатки.
Адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так какнекоторые из них используются прирасчете различных критериев адекватности.
|
Характеристики точности
Под точностью понимается величина случайных ошибок. Сравнительный анализ точности имеет смысл только для адекватных моделей: среди них лучшей признается модель с меньшими значениями характеристик точности, к которым относятся:
- максимальная ошибка 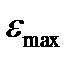 соответствует максимальному отклонению расчетных значений от фактических;
соответствует максимальному отклонению расчетных значений от фактических;
- средняя абсолютная ошибка 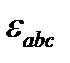
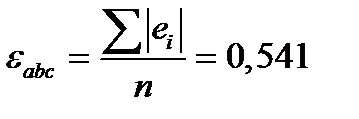 (2.14)
(2.14)
показывает, насколько в среднем отклоняются фактические значения от модели;
- средняя относительная ошибка 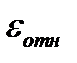
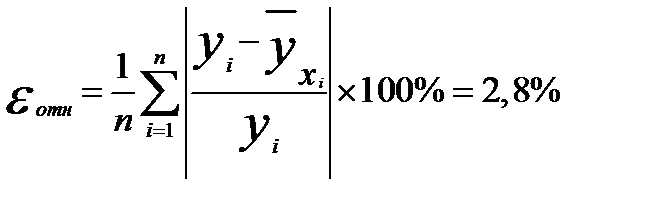 ;(2.15)
;(2.15)
- остаточная дисперсия
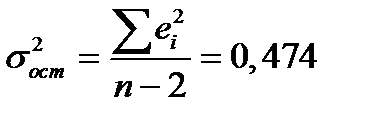 ; (2.16)
; (2.16)
- средняя квадратическая ошибка
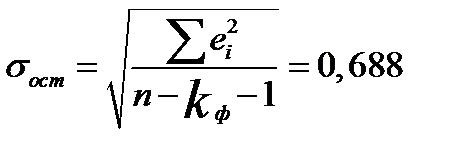 . (2.17)
. (2.17)
Средняя квадратическая ошибка является наиболее часто используемой характеристикой точности (что объясняется ее связью с остаточной дисперсией, которая играет центральную роль в регрессионном анализе). Значение средней квадратической ошибки всегда несколько больше значения средней абсолютной ошибки, но они имеют схожий смысл – характеризуют среднюю удаленность расчетных значений модели от фактических исходных данных. Обычно точность модели признается удовлетворительной если выполняется условие:
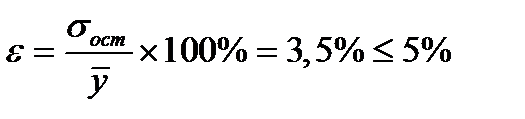 . (2.18)
. (2.18)
К характеристикам точности можно отнести также множественный коэффициент детерминации
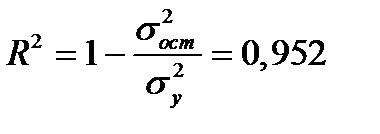 , (2.19) характеризующий долю дисперсии зависимой переменной, объясненной с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):
, (2.19) характеризующий долю дисперсии зависимой переменной, объясненной с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):
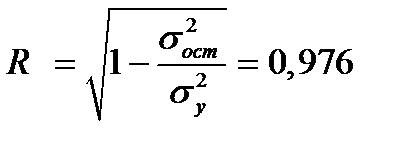 . (2.20)
. (2.20)
В случае парной линейной регрессии значение множественного коэффициента корреляции совпадает с линейным коэффициентом корреляции.
Проверка нормальности ряда остатков может быть выполнена приближенно по условиям (7.2). В связи с тем, что каждый из относительных показателей формы распределения ( 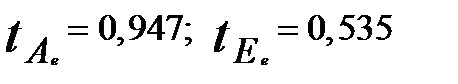 ) меньше 1,5 эмпирическое распределение ряда остатков не противоречит нормальному.
) меньше 1,5 эмпирическое распределение ряда остатков не противоречит нормальному.
Проверка адекватности модели
Проверка адекватности модели заключается в определении её значимости и наличии или отсутствии систематической ошибки.
Сначала проверяется значимость параметров уравнения. Если, например, параметр 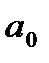 является незначимым, то необходимо с помощью метода наименьших квадратов получить соответствующее уравнение из которого определяется значение параметра
является незначимым, то необходимо с помощью метода наименьших квадратов получить соответствующее уравнение из которого определяется значение параметра 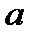 .
.
Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.
Средняя ошибка параметра 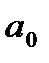 равна:
равна:
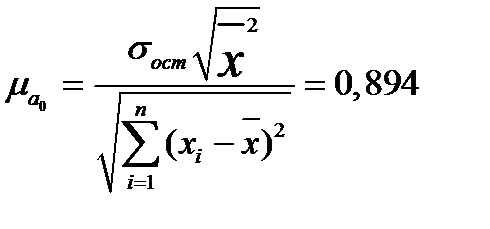 , (2.21)
, (2.21)
а для параметра 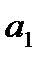 :
:
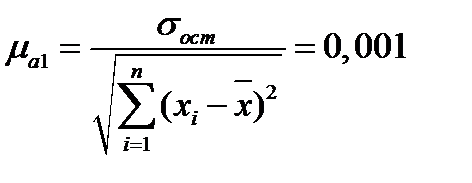 . (2.22)
. (2.22)
Расчетные значения t- критерия вычисляются по формуле:
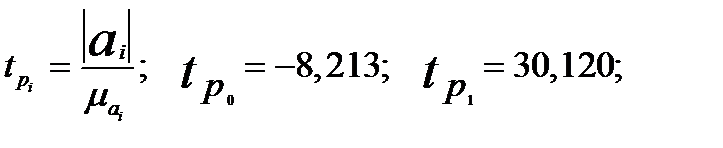 (2.23) Параметр считается значимым, если
(2.23) Параметр считается значимым, если 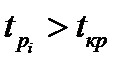 . Значение
. Значение 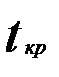 определяется по табл. 6 Практикума. Входами в табл. являются уровень значимости
определяется по табл. 6 Практикума. Входами в табл. являются уровень значимости 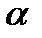 и количество степеней свободы
и количество степеней свободы 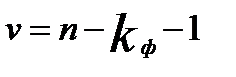 , где
, где 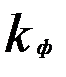 - количество факторов в уравнении регрессии. При
- количество факторов в уравнении регрессии. При 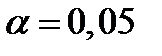 и
и 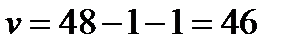
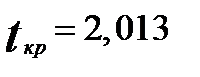 . Следовательно, в рассматриваемом примере параметры
. Следовательно, в рассматриваемом примере параметры 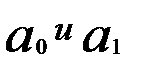 являются значимыми.
являются значимыми.
Параметр 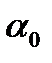 лежит в пределах
лежит в пределах 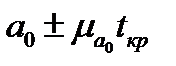 ;
; 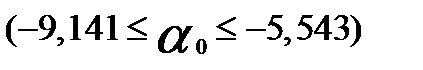 ,
,
а параметр 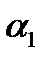 -
- 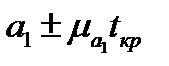 ;
; 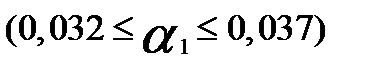 .
.
Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:
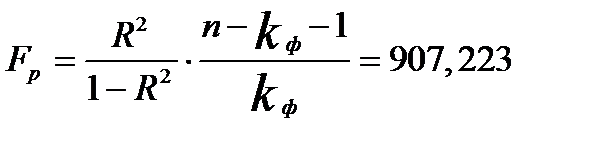 (2.24)
(2.24)
Расчетное значение F сопоставляется скритическим 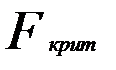 для числа степеней свободы
для числа степеней свободы 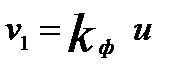
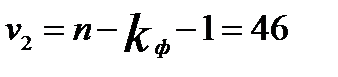 при заданном уровне значимости
при заданном уровне значимости  (например,
(например, 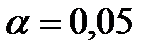 ),где
),где 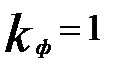 .
. 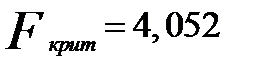 .
.
Если 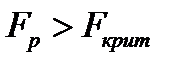 , то уравнение считается значимым.
, то уравнение считается значимым.
Проверка наличия или отсутствия систематической ошибки
Проверка свойства нулевого среднего.
Рассчитывается среднее значение ряда остатков
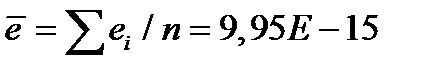 . (2.25)
. (2.25)
Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию. Если средняя ошибка не точно равна нулю, то для определения степени ее близости к нулю используется t – критерий Стьюдента. Расчётное значение критерия вычисляется по формуле
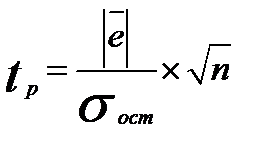 (2.26)
(2.26)
и сравнивается с критическим 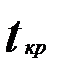 .Если выполняется неравенство
.Если выполняется неравенство 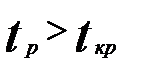 , то модель неадекватна по данному критерию.
, то модель неадекватна по данному критерию.
Проверка случайности ряда остатков.
Осуществляется по методу серий. Серией называется последовательность расположенных подряд значений ряда остатков, для которых разность 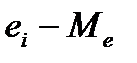 (графа 4 табл. 7.4) имеет один и тот же знак, где
(графа 4 табл. 7.4) имеет один и тот же знак, где 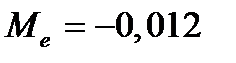 - медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы.
- медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы.
Если модель хорошо отражает исследуемую зависимость, то она часто пересекает линию графика исходных данных и тогда серий много, а их длина невелика. Иначе – серий мало и некоторые из них включают большое число членов.
В качестве серий рассматриваются расположенные подряд ошибки с одинаковыми знаками. Далее подсчитывается число серий 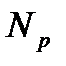 и длина максимальной из них
и длина максимальной из них 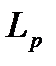 . Полученные значения сравниваются с критическими
. Полученные значения сравниваются с критическими
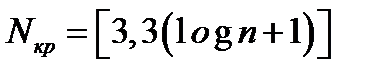 (2.27)
(2.27) 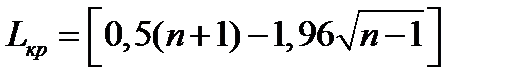 (2.28) (квадратные скобки означают округление вниз до ближайшего целого).
(2.28) (квадратные скобки означают округление вниз до ближайшего целого).
Если выполняется система неравенств:
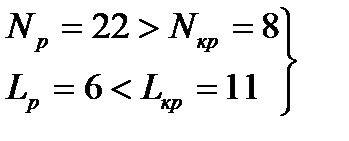 , (2.29) то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.
, (2.29) то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.
Проверка независимости последовательных остатков.
Является важнейшим критерием адекватности модели и осуществляется с помощью коэффициента Дарбина-Уотсона:
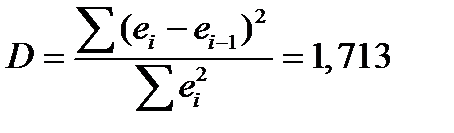 . (2.30) Для рядов с тесной взаимосвязью между последовательными значениями остатков значение
. (2.30) Для рядов с тесной взаимосвязью между последовательными значениями остатков значение 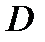 близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.
близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.
Если последовательные остатки независимы, то 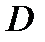 близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.
близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.
При отрицательной автокорреляции остатков (строго периодичном чередовании их знаков) 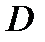 близко к 4.
близко к 4.
Для проверки существенности положительной автокорреляции остатков значение 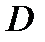 сравнивается с
сравнивается с 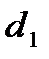 и
и 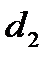 из табл. 2 Приложения к лекции:
из табл. 2 Приложения к лекции:
если 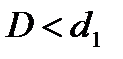 , то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
если 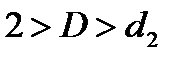 , то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию(в рассматриваемом примере
, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию(в рассматриваемом примере 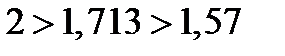 );
);
если 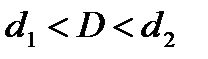 , то значение критерия лежит в области неопределенности.
, то значение критерия лежит в области неопределенности.
Если 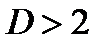 , то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не
, то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не 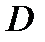 , а
, а 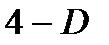 и делаются аналогичные выводы.
и делаются аналогичные выводы.
Проверка постоянства дисперсии остатков.
Если на графике остатков они укладываются в симметричную относительно нулевой линии полосу шириной 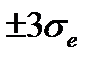 (модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.
(модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.
Значения стандартных остатков вычисляются по формуле
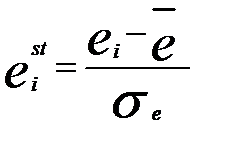 , где
, где 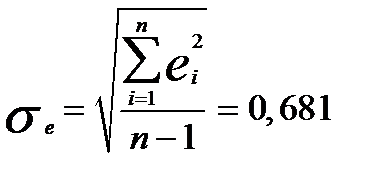 и приведены в графе 5 табл.1.1.
и приведены в графе 5 табл.1.1.
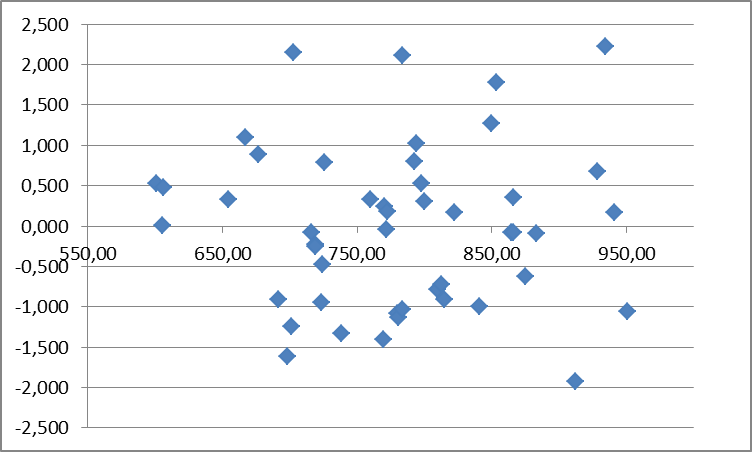
Рис. 2.1. График стандартных остатков
Кроме визуальной оценки постоянства дисперсии существуют и более точные методы, например, тест Гольдфельда-Квандта. Суть теста заключается в следующем. Все n наблюдений упорядочиваются по возрастанию значений независимой переменной (x) и производится оценка параметров регрессий для первых 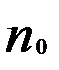 и последних
и последних 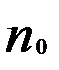 наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение
наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение 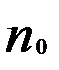 порядка n/3. Далее вычисляется расчётное значение статистики Фишера
порядка n/3. Далее вычисляется расчётное значение статистики Фишера
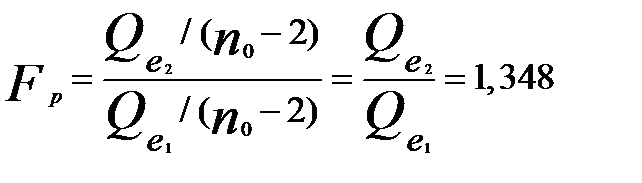 ,(2.31)
,(2.31)
где 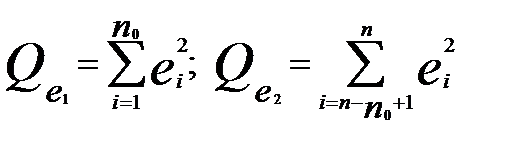 - суммы квадратов остатков для первых
- суммы квадратов остатков для первых 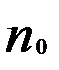 и последних
и последних 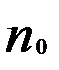 наблюдений соответственно. Далее задаётся уровень значимости
наблюдений соответственно. Далее задаётся уровень значимости 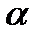 и определяется
и определяется 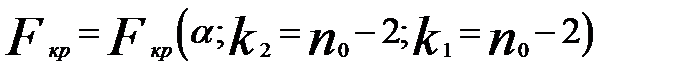 с помощъю статистических таблиц.
с помощъю статистических таблиц. 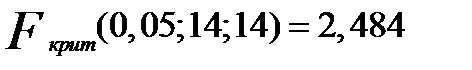 .
.
Если 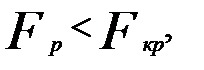 то делается вывод о постоянстве дисперсии.
то делается вывод о постоянстве дисперсии.
По совокупности четырех критериев делается вывод о принципиальной возможности использования модели: если модель адекватна по критериям постоянства дисперсий и нулевого среднего и хотя бы по одному из двух других критериев, то она может быть принята для использования, хотя и не признается полностью адекватной.
Построение доверительных интервалов
Конечной целью моделирования является оценка или прогнозирование показателя Yв зависимости от значений X.
Прогноз подразделяется на точечный и интервальный и обычно осуществляется не более чем на одну треть размаха:
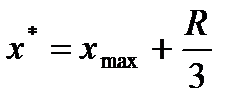 ,
,
где 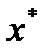 - точка прогноза.
- точка прогноза.
В точечном прогнозе показателя Yдля 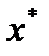 определяется лишь одно число, которое представляет условное среднее и (при выполнении предпосылок регрессионного анализа) наиболее вероятное значение с точки зрения закономерности, отраженной в модели. В таком прогнозе не учитываются отклонения от закономерностей в результате воздействия случайных и неучтенных факторов.
определяется лишь одно число, которое представляет условное среднее и (при выполнении предпосылок регрессионного анализа) наиболее вероятное значение с точки зрения закономерности, отраженной в модели. В таком прогнозе не учитываются отклонения от закономерностей в результате воздействия случайных и неучтенных факторов.
В интервальном прогнозе отклонения от закономерностей в результате случайных воздействий определяются границами доверительных интервалов.
Доверительным интервалом называется такой интервал, которому с заданной степенью вероятности (называемой доверительной) принадлежат истинные значения показателя при условии, что закономерности, отраженные в модели, не противоречат развитию как на участке наблюдения, так и на участке оценки (или в периоде упреждения прогноза).
Случайные отклонения от модели проявляются в виде ошибок. Поэтому при определении границ, доверительных интервалов необходимо определить из чего складываются возможные ошибки моделирования, оценки и прогнозирования. При условии, что модель адекватна, и возможные ошибки носят случайный характер, следует различать два основных источника ошибок:
ошибки аппроксимации (рассеяние наблюдений относительно модели);
ошибки оценок параметров модели.
Наличие ошибок первого типа очевидно даже визуально. Величина ошибок аппроксимации характеризуется остаточной дисперсией 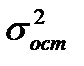 или средней квадратической ошибкой
или средней квадратической ошибкой 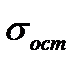 . Распределение этих ошибок для адекватных моделей – нормально (нормальность ошибок – одно из условий адекватности).
. Распределение этих ошибок для адекватных моделей – нормально (нормальность ошибок – одно из условий адекватности).
Ошибки оценок параметров модели обусловлены тем, что их параметры, фиксированные в модели как однозначные, в действительности являются случайными величинами, так как они оцениваются на основе фактических данных, в которых присутствует как закономерная, так и случайная составляющие. Средние значения этих оценок при выполнении предпосылок регрессионного анализа соответствует истинным значениям параметров, а их дисперсии зависят от остаточной дисперсии, числа наблюдений и вида модели.
Общее среднее квадратическое отклонение истинных значений от расчетных может быть представлено как:
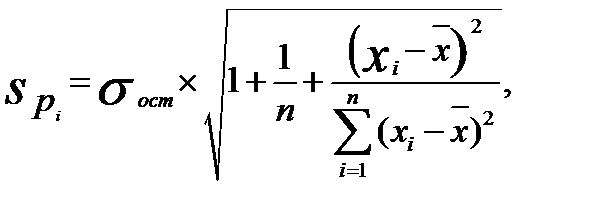 (2.32)
(2.32)
а в точке прогноза:
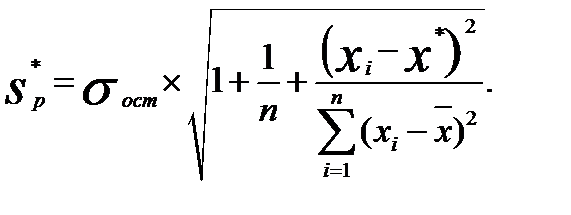 (2.33)
(2.33)
Исходя из предпосылки нормального распределения остатков границы доверительных интервалов определяются по формулам:
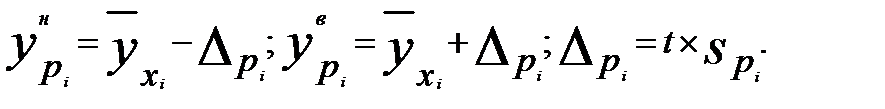 (2.34)
(2.34)
Анализ выражений (2.32, 2.33) позволяет для моделей парной регрессии сделать вывод, что доверительные интервалы тем шире, чем:
- больше остаточная дисперсия (менее точна модель);
- значение 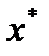 больше удалено от среднего значения
больше удалено от среднего значения 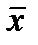 (см. рис. 2.32);
(см. рис. 2.32);
- сложнее форма модели;
- больше заданная доверительная вероятность.
Обобщая полученные результаты, можно сделать вывод, что построенная модель обладает хорошим качеством, т.е. она достаточно точна и адекватна исследуемому процессу по всем перечисленным ранее критериям. Учитывая еще и нормальность ряда остатков можно осуществлять точечный и интервальный прогнозы. В связи с этим табл. 2.2 приведены данные для построения доверительных интервалов.
Массив
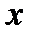 дополнен двумя значениями:
дополнен двумя значениями: 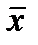 и
и 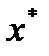 , которые выделены жирным шрифтом. Значения:
, которые выделены жирным шрифтом. Значения: 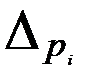 - ширина доверительного интервала;
- ширина доверительного интервала; 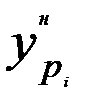 - нижняя граница доверительного интервала;
- нижняя граница доверительного интервала; 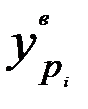 - верхняя граница доверительного интервала вычислены по формулам (2.34) с доверительной вероятностью 0,975 и соответствующим ей коэффициентом доверия Стьюдента 2,315. Выбор распределения Стьюдента обусловлен достаточно большим значением относительного показателя асимметрии остатков.
- верхняя граница доверительного интервала вычислены по формулам (2.34) с доверительной вероятностью 0,975 и соответствующим ей коэффициентом доверия Стьюдента 2,315. Выбор распределения Стьюдента обусловлен достаточно большим значением относительного показателя асимметрии остатков.
График доверительных интервалов и график их ширины приведены на рис. 2.1 и 2.2.
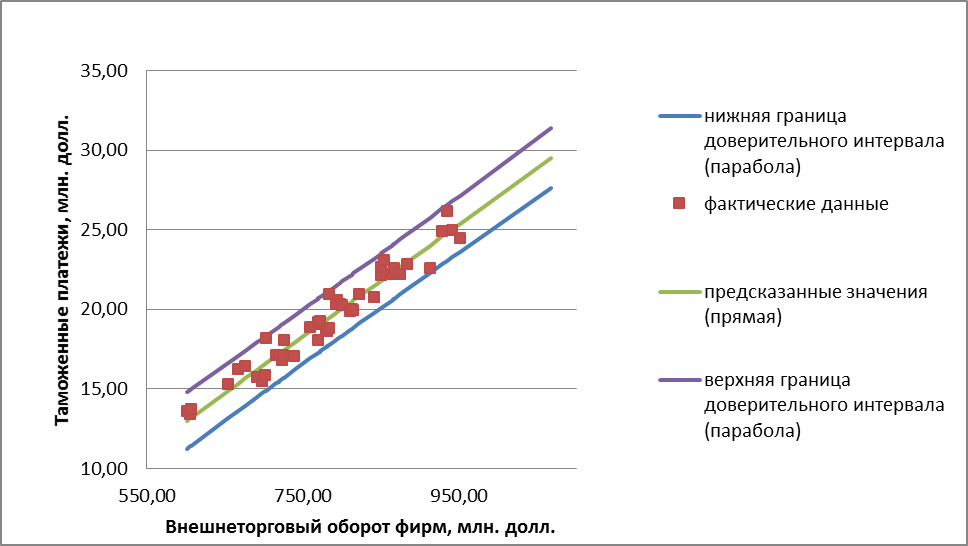

Рис. 2.2.График доверительных интервалов
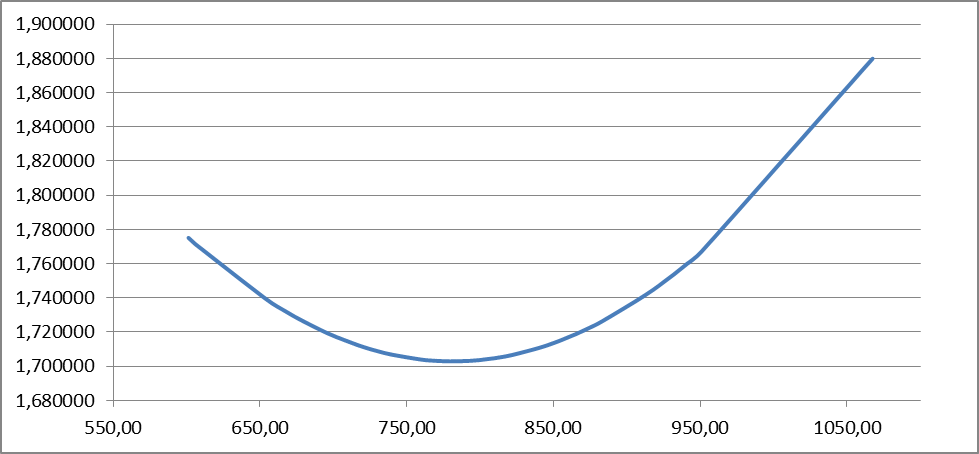

Рис. 2.3. График ширины доверительных интервалов
С учетом нормального распределения остатков при среднем значении ВТО фирм равном 1067,43 млн. долл. с вероятностью 0,975 прогнозируемые таможенные платежи в бюджет составят от 27,61 до 31,37 млн. долл., при этом условное среднее (наиболее вероятный объём поступлений) ожидается 29,49 млн. долл.
Лекция №3
Дата добавления: 2016-03-22; просмотров: 1474;
