Классическая вероятность
Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом.
Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление такого события.
Количественной мерой возможности появления некоторого случайного события служит вероятность.
При классическом определении за вероятность события А принимается отношение числа благоприятствующих этому событию элементарных исходов (m) к общему числу возможных исходов (n): 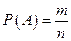 .
.
Классическая вероятность обладает следующими свойствами:
1) вероятность достоверного события равна единице;
2) вероятность невозможного события равна нулю;
3) вероятность случайного события определяется неравенством 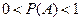 .
.
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики:
- если составляются такие комбинации из n элементов по m, которые отличаются друг то друга только составом элементов, то они называются сочетаниями
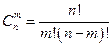 ;
; - если комбинации отличаются и составом элементов, и порядком их следования, то они называются размещениями:
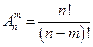 ;
; - если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками:
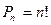 .
.
Дата добавления: 2016-03-22; просмотров: 841;
