Полигон и гистограмма

Наблюдаемые данные, представленные в виде вариационного ряда, можно изобразить графически. Если вариационный ряд дискретной случайной величины представить в виде ломанной линии, связывающей на плоскости точки с координатами 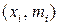, то такой график называют полигоном.

Интервальный вариационный ряд графически изображают с помощью гистограммы. Для ее построения в прямоугольной системе координат на оси абсцисс откладывают отрезки частичных интервалов варьирования и на этих отрезках как на основаниях строят прямоугольники с высотами, равными частотам или относительным частотам соответствующих интервалов.

Графическое представление вариационных рядов в виде полигона и гистограммы позволяет получить первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.

Точечные оценки

Оценки параметров генеральной совокупности, полученные на осно­вании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, она называется точечной. К чис­лу таких оценок относятся выборочная средняя и выборочная диспер­сия.

Выборочная средняяопределяется как среднее арифметическое по­лученных по выборке значений:

,

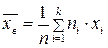где 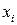– варианта выборки; 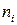– частота варианты; 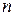– объем выборки.

Выборочная дисперсияпредставляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней: .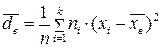

Статистическая оценка является случайной величиной и меняется в зависимости от выборки. Если математическое ожидание статистиче­ской оценки равно оцениваемому параметру генеральной совокупности, то такая оценка называется несмещенной,если не равно – то смещен­ной.

Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку. Выбо­рочная дисперсия оценивает дисперсию генеральной совокупности и яв­ляется смещенной оценкой.

Для устранения смещенности выборочной дисперсии ее умножают на величину 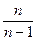и получают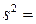 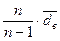. Величину 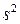называют несмещеннойили «исправленной» выборочной дисперсией.