Распределение частот
Совокупность всех возможных объектов данного вида, над которыми проводятся наблюдения, или совокупность всех возможных наблюдений, проводимых в одинаковых условиях над некоторой случайной величиной, называется генеральной совокупностью. Генеральная совокупность может содержать конечное или бесконечное число элементов. Отобранные из генеральной совокупности объекты (результаты наблюдений над конечным числом объектов из генеральной совокупности) называются выборочной совокупностьюили выборкой. Число N элементов генеральной совокупности и число п элементов выборочной совокупности будем называть объемамигенеральной и выборочной совокупности соответственно.
Расположение выборочных наблюденных значений случайной величины в порядке неубывания называется ранжированием.
Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой,а изменение этого значения – варьированием.
Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотойварианты. Если 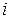 – индекс варианты, то
– индекс варианты, то 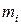 – число измеренных значений i-й варианты, отношение
– число измеренных значений i-й варианты, отношение 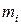 к общей сумме частот всех вариант
к общей сумме частот всех вариант 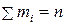 называется относительной частотойварианты и обозначается
называется относительной частотойварианты и обозначается 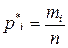 .
.
Дискретным вариационным рядомраспределения (распределением частот) называется ранжированная совокупность вариант 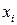 с соответствующими им частотами или относительными частотами.
с соответствующими им частотами или относительными частотами.
Если наблюдаемая случайная величина непрерывна или дискретная величина такова, что число ее возможных значений велико, то для построения вариационного ряда используют интервальный ряд распределения. В этом случае весь возможный интервал варьирования разбивают на конечное число частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.
Интервальным вариационным рядом называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений случайной величины.
Дата добавления: 2016-03-22; просмотров: 661;
