Согласно закону Ома, ток КЗ для аккумуляторной батареи будет
Iк.з = Е ⁄R0 = 220 ⁄2 = 110 А,
с учетом условия выбора берем плавкую вставку с током срабатывания
Iн.вст = 10 А ≤ 0,1Iк.з = 0,1·110 = 11 А.
Пример № 1.4
Выбрать из номинального ряда 0,5; 0,75; 1,0; 1,5; 2,5; 4; 6; 10: 16 мм2 величину сечения медных соединительных проводов по нагреву для номинального режима нагрузки (см. пример № 1.2) при условии допустимой плотности тока Jдоп = 7 А ⁄мм2.
Решение
Сечение провода должно удовлетворять условию:
S ≥ IН ⁄Jдоп ≥ 16,9 ⁄7 ≥ 2,41 мм2,
Выбираем медный провод сечением SН = 2,5 мм2.
Пример № 1.5
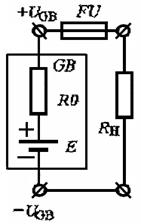 Определить для схемы (см. рис. п1.5.1) значение к.п.д. η и произведенного тепла Q в течение 8 часов в киловатт-часах, килоджоулях и килокалориях. Известно, что э.д.с. аккумулятора Е равна 220 В, его внутреннее сопротивление R0 равно2 Ом, а сопротивление нагрузки RH равно 20 Ом.
Определить для схемы (см. рис. п1.5.1) значение к.п.д. η и произведенного тепла Q в течение 8 часов в киловатт-часах, килоджоулях и килокалориях. Известно, что э.д.с. аккумулятора Е равна 220 В, его внутреннее сопротивление R0 равно2 Ом, а сопротивление нагрузки RH равно 20 Ом.
Рис. п1.5.1. Схема цепи с эквивалентным сопротивлением нагрузки RH
Решение
Находим ток, мощности и потребленную энергию за 8 часов:
I = E ⁄ (R0 + RH) = 220 ⁄ (2 + 20) = 20 A;
PН = RH I 2 = 20∙202 = 8 000 Вт = 8 кВт;
PИ = (R0 + RH) I 2 = (2+20)∙20 2 = 8 800 Вт = 8,8 кВт;
WH = PН · t = 8·8 = 64 кВт·ч;
QH = 864·WH ≈ 864·64 = 55 296 ккал ≈ 231513,3 кДж.
Коэффициентом полезного действия (к.п.д.) η электрической цепи является отношение мощности приемника PН к мощности источника э.д.с. PИ
η = PН ⁄PИ = 8 000 ⁄8 800 = 0,91.
Пример № 1.6
Для электрической цепи (см. рис. п1.5.1) построить графики изменения напряжения UGB, мощности батареи PGB, мощности нагрузки PНи η в зависимости от тока I при изменении сопротивления RH от бесконечности (режим «холостого хода») до нуля (режим «короткого замыкания»).
Решение
Так как для данной цепи
Iк.з = Е ⁄ R0 = 220 ⁄2 = 110 А;
I = E ⁄ (R0 + RH);
UGB = E – R0I = 220–2I;
PGB = EI = 220I;
PН = (E – R0I)I = (220–2I)I;
η = 1 – R0I ⁄E = 1–2I ⁄220,
то соответствующие функции этих графиков в диапазоне 0÷110 А имеют вид, представленный на рисунке п1.6.1.
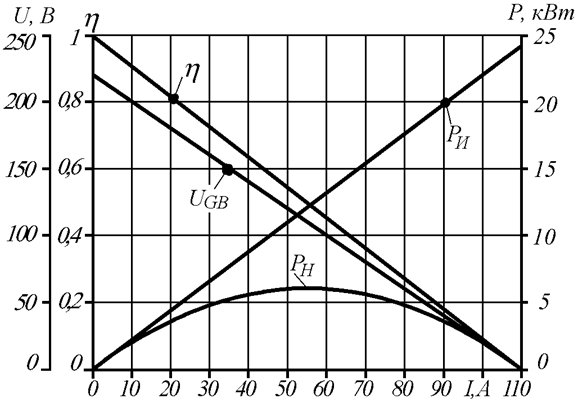
Рис. п1.6.1. Энергетические диаграммы электрической цепи
Примечание.Для построения графиков следует привести таблицу расчетных данных функций минимум в 5 точках диапазона тока I.
Пример № 1.7
Для электрической цепи (см. рис. п1.5.1) построить в совмещенной системе координат графики нормированных статических характеристик мощности PИ/PИК источника питания, мощности PН/PИК нагрузки приемника и к.п.д. η в функции величины отношения сопротивления приемника к внутреннему сопротивлению источника э.д.с. RН/RВТ.
Решение
Для данной цепи, используя законы Ома и Джоуля-Ленца, определим величины нормированных характеристик в диапазоне RН/RВТ от 0 до 6 (см. табл. п1.7.1) и построим в совмещенной системе координат соответствующие графики (см. рис. п1.7.1).
Таблица п1.7.1
| Параметр | Точки графиков | ||||||
| RН/RВТ | |||||||
| PИ, Вт | *24200 | ||||||
| PН, Вт | |||||||
| η | 0,5 | 0,67 | 0,75 | 0,8 | 0,83 | 0,86 | |
| PИ/PИК | 0,5 | 0,34 | 0,25 | 0,2 | 0,17 | 0,14 | |
| PН/PИК | 0,25 | 0,23 | 0,19 | 0,16 | 0,14 | 0,12 |
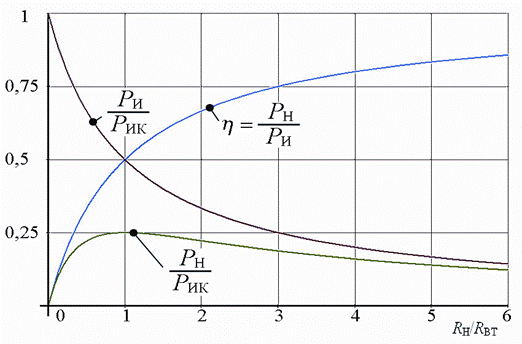
Рис. п1.7.1. Нормированные статические характеристики
электрической цепи
Пример № 2.1
С помощью градуировочных кривых (см. рис. 2.2 и 2.3) определить значения сопротивлений металлических термометров сопротивления градуировок 20, 21, 22, 23 и 24 при температуре 150ºС.
Решение
Определение ожидаемых значений сопротивления температурозависимых резисторов по номограммам (градуировочным кривым) является стандартной инженерной процедурой. Для данного примера соответствующие номограммы с ключами графического определения значений металлических термометров при температуре 150ºС приведены на рисунке п8.1.
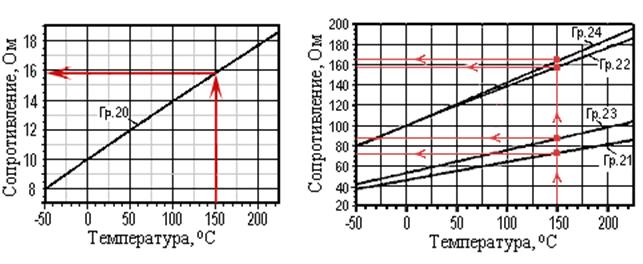
Рис. п2.1.1. Номограммы определения сопротивления
металлических термометров с ключами для температуры 150ºС
Из номограмм следует, что при температуре 150ºС сопротивления термометров будут:
гр. 20 15,5 Ом;
гр. 21 71 Ом;
гр. 22 157 Ом;
гр. 23 88 Ом;
гр. 24 165 Ом.
Пример № 2.2
В цепи постоянного тока (рис. п2.2.1) определить энергетические параметры резистора R3. Известно, что Е = 220 В; R0 = 2 Ом; R1 =50 Ом; R2=150 Ом; R3 = 20 Ом; R4=70 Ом; R3 = 10 Ом.
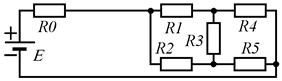
Рис. п2.2.1. Схема электрической цепи с мостовым соединением
резисторов нагрузки потребителя
Решение
Мостовая цепь является типичным примером сложного соединения, которое нельзя отнести ни к последовательному, ни к параллельному. В типичном изображении схема замещения мостовой цепи (а) и ее эквивалентная схема для выполнения различных расчетов показаны на рисунке п2.2.2.
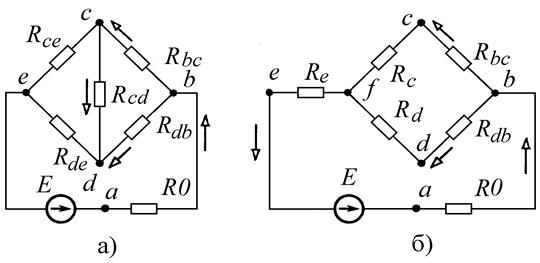
Рис. п2.2.2. Схема мостовой цепи (а) и ее схема замещения (б)
По условию надо определить ток, напряжение и мощность на резисторе R3, которому в типовой схеме соответствует резистор Rсd. Для этого надо вычислить разность потенциалов между узлами "c" и "d", что удобно сделать, используя эквивалентную замену трех ветвей, соединенных треугольником (например, e,c,d), трехлучевой звездой с ветвями из резисторов Re, Rc, Rd (рис. п2.2.2б). Мостовая схема преобразуется в цепь с последовательным и параллельным соединением элементов.
Эквивалентное преобразование треугольника в звезду выполняется по формулам:
Re = RceRde ⁄ (Rce + Rde + Rcd),
Rc = RceRcd ⁄ (Rce + Rde + Rcd),
Rd = RdeRcd ⁄ (Rce + Rde + Rcd).
Далее, применив (см. рис. п2.2.3) формулы расчета сопротивлений, токов и напряжений в последовательных и параллельных соединений резисторов, получим потенциалы узлов "c" и "d" . После чего вычислим энергетические параметры резистора R = Rcd:
- напряжение UR3 = Uec – Ued;
- ток IR3 = UR3 ⁄R3;
- мощность РR3 = IR3 ∙ UR3.
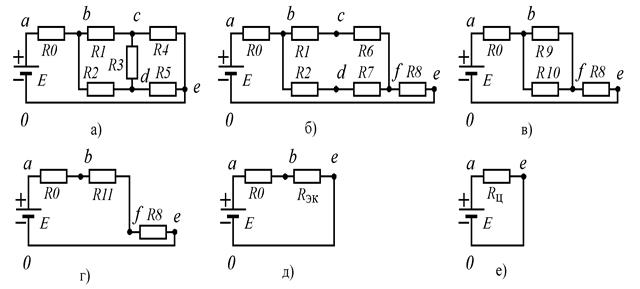 Рис. п2.2.3. Схемы поэтапного замещения мостовой цепи
Рис. п2.2.3. Схемы поэтапного замещения мостовой цепи
ее эквивалентной схемой
Таблица п2.2.1
Дата добавления: 2016-03-20; просмотров: 1068;
