Исходя из условия резонанса напряжений

U_L = U_C,или X_L = Х_C, или Lω = 1 ⁄Cω, или 2πfL = 1 ⁄2πfC

имеем:

C = 1 ⁄4π²f²L = 1 ⁄4π²100²2 ∙≈ 1,27∙10^-6 Ф = 1,27 мкФ.

Пример № 3.2

Для схемы замещения электрической цепи конденсаторной обмотки LM2 однофазного двигателя (рис. п3.1.1б) определить действующие значения тока I, напряжений Ur, Ul, Uc, коэффициента мощности λ (cosφ), полной мощности S, активной мощности Р и реактивной мощности Q. Известно, что U = 200 B; R = 500 Ом; L = 2 Гн; C = 3 мкФ; f = 100 Гц.

Решение

В соответствии со вторым законом Кирхгофа и законом Ома, записанных в комплексной форме, имеем

Ú = Ú_R + Ú_L+ Ú_C,

или

Ú = RÍ + jX_LÍ + (-jX_C)Í = (R + jX_L - jX_C)Í,

или

Ú = ZÍ.

Комплекс Z является эквивалентным комплексным сопротивлением цепи:

Z = R + jX_L – jX_C.

Используя формулы расчета реактивных сопротивлений емкостного и индуктивного элементов, получим:

X_L =2πfL = 2π100·2 ≈ 1 256,6 Ом,

X_C. =1 ⁄2πfС = 1 ⁄2π100·3·10^-6 ≈ 530,5 Ом

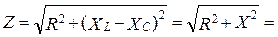= 500² + (1 256,6 - 530,5)² ≈ 881,6 Ом.

Действующие значения напряжения Ur, Ul, Uc:

U_R = R∙I = 500∙0,227 ≈ 113,5 B,

U_L = X_L∙I = 1 256,6∙0,227 ≈ 285,3 B,

U_C = X_C ∙I = 530,5∙0,227 ≈ 120,4 B.

Активная мощность цепи:

Р = R∙I ² = 500∙0,227 ² ≈ 25,8 Bт.

Реактивная мощность цепи:

Q = (X_L - X_C)∙I ²= (1 256,6 - 530,5)∙0, 227 ² ≈ 37,4 вар.

Полная мощность цепи:

S = U∙I = 200∙0,227 ≈ 45,4 BA.

Коэффициент мощности цепи:

λ = cosφ = P ⁄S = 25,8 ⁄45,4 ≈ 0,57.

Пример № 3.3

Для схемы замещения электрической цепи конденсаторной обмотки LM2 однофазного двигателя (рис. п3.1.1б), построить в комплексной системе координат треугольник сопротивлений, треугольник мощностей и топографическую диаграмму. Данные для построения диаграмм взять из примера № 3.2.

Решение

Для построения диаграмм (см. рис. п3.3.1) используем полярную систему координат. Масштабы для построения векторов приведены рядом с соответствующими диаграммами.

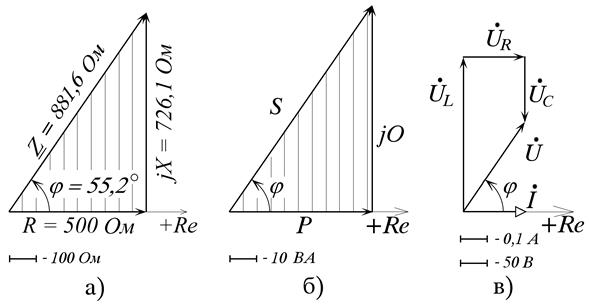
а - треугольник сопротивлений;

б - треугольник мощностей;

в - топографическая диаграмма

Рис. п3.3.1. Энергетические диаграммы цепи (векторные)

Пример № 4.1

Для последовательного соединения катушки индуктивности и реостата (рис. п4.1.1) составить схемы замещения последовательного и параллельного типа, а также построить их векторные диаграммы. Известно, что U = 220 B; R_К = 10 Ом; L_К = 2 Гн; R = 200 Ом; С = 5 мкФ; f = 100 Гц.

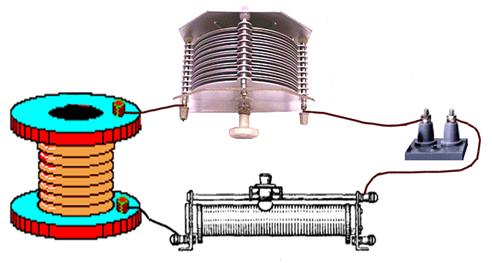
Рис. п4.1.1. Монтажная схема соединения

Решение

Принципиальная исходная схема электрической цепи, представленной на рисунке п4.1.1, а также эквивалентные схемы ее замещения последовательного и параллельного типов, представлены на рисунке п4.1.2.

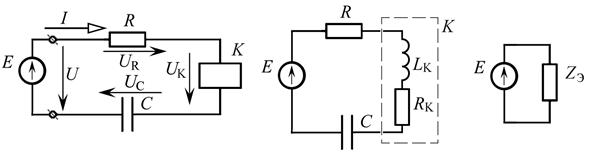
а) б) в)

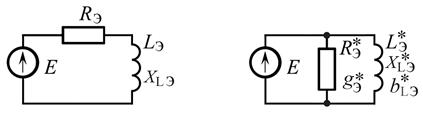
г) д)

а – исходная схема цепи;

б – подробная схема замещения;

в – свернутая схема замещения;

г – эквивалентная схема замещения последовательного типа;

д – эквивалентная схема замещения параллельного типа

Рис. п4.1.2. Принципиальная исходная схема цепи и ее схемы замещения

Реактивное (индуктивное) сопротивление цепи в эквивалентной схеме замещения последовательного типа (рис. п4.1.2г) будет равно

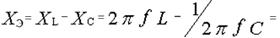
= 2·3,14·100·2 – 1/(2·3,14·100·5·10^–6) ≈ 1257 – 318 = 939 Ом.

Активное (резистивное) сопротивление цепи в эквивалентной схеме замещения последовательного типа будет равно

R_Э = R + R_K = 200 + 10 = 210 Ом.

Полное (комплексное) сопротивление цепи будет равно

Z_Э = R_Э + jX_Э = 210 + j 939 = 962,2·e^j^77,4° Ом.

Ток (действующий) в цепи эквивалентной схемы замещения последовательного типа будет равен

İ = Ů/Z_Э = 220·e^j0°/962,2·e^j77,4° =

0,229·e^{– j77,4°} = 0,05 – j 0,223 A.

Падения напряжения на элементах цепи будут равны:

- на активном сопротивлении

Ů_R_Э = İ·R_Э = 0,229·e^–^j^77,4° · 210·e^j^0° = 48,09·e^–^j^77,4° B;

- на реактивном (индуктивном) сопротивлении

Ů_X_Э = İ·X_Э = 0,229·e^–^j^77,4° · 939·e^j^90° = 215,03·e^–^j^12,6° B.

Соответствующая векторная диаграмма тока и напряжений (ВДТН) приведена на рисунке п4.1.3а). Для удобства построения векторов на диаграмме вектор тока İ совмещен с положительной вещественной полуосью Re комплексной плоскости.

Расчет цепи с эквивалентной схемой замещения параллельного типа (рис. п4.1.2д) выполняем с использованием метода эквивалентных проводимостей (проводимость – величина, обратная сопротивлению).

Эквивалентная проводимость рассчитываемой цепи будет равна

Y_Э = 1/Z_Э = 1·e^j^0°/962,2·e^j^77,4° ≈

≈ 0,00104·e^–^j^77,4° = 0,00023 – j 0,001015 См.

Ток (действующий) в цепи будет равен

İ = Ů·Y_Э = İ _R_*Э + jİ _X_*_L_Э =

220·e^j^0°·0,00104·e^–^j^77,4° = 0,229·e^–^j^77,4° = 0,05 – j 0,223 A.

С учетом этого выражения токи в ветвях цепи эквивалентной схеме замещения параллельного типа будут равны:

- в активной проводимости (активное сопротивление R*_Э)

İ _R_*Э = Ů/R^*_Э = Ů·g^*_Э = 0,05· e^j^0° А;

- в реактивном (индуктивном) сопротивлении

İ _X_*_L_Э = Ů/ X*_L_Э = Ů·b^* _L_Э = 0,223 · e^–^j^90° А.

Соответствующая векторная диаграмма токов и напряжения (ВДТН) приведена на рисунке п4.1.3б. Для удобства построения векторов на диаграмме вектор напряжения Ů совмещен с положительной вещественной полуосью Re комплексной плоскости.

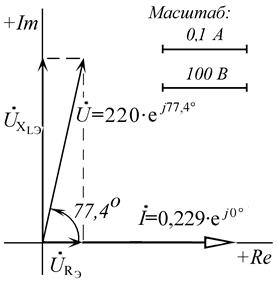
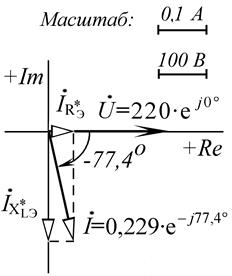
а) б)

а – ВДТН эквивалентной схемы замещения последовательного типа;

б – ВДТН эквивалентной схемы замещения параллельного типа

Рис. п4.1.3. ВДТН в схемах замещения

Пример № 4.2

Для параллельного двух потребителей, имеющих эквивалентные комплексные сопротивления Z_Э1 и Z_Э2 (рис. п4.2.1), составить схему замещения параллельного типа и построить ее векторные диаграммы напряжения и токов. Известно, что U = 220 B; Z_Э1 = 962,2·e^j^77,4° Ом; Z_Э2 = 500·e^–^j^45°.

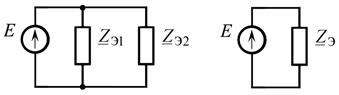
Рис. п4.2.1. Исходная и эквивалентная схемы электрической цепи

Решение

Определим вначале комплексные проводимости потребителей.

Эквивалентная проводимость первого потребителя будет равна

Y_Э1 = 1/Z_Э1 = 1·e^j^0°/962,2·e^j^77,4° ≈

≈ 0,00104·e^–^j^77,4° = 0,00023 – j 0,001015 См.

Эквивалентная проводимость второго потребителя будет равна

Y_Э2 = 1/Z_Э2 = 1·e^j^0°/500·e^–^j^45° ≈

≈ 0,002·e^45° = 0,00141 + j 0,00141 См.

Эквивалентная проводимость всей нагрузки будет равна

Y_Э=Y_Э1+Y_Э2 =G_Э1+G_Э2+B_Э1+B_Э2=(g_Э1+g_Э2)+j(b_Э1+b_Э2)=

=(0,00023 + 0,00141) + j(–0,001015 + 0,00141) ≈

≈ 0,00164 + j·0,000395 ≈ 0, 001687·e^j^13,5° См.

Положительное значение мнимой составляющей эквивалентной проводимости нагрузки указывает на емкостной характер её реактивного сопротивления.

Ток (действующий) в цепи будет равен

İ=Ů·Y_Э=220·e^j0°·0,001687·e^j13,5°=0,37114·e^j13,5°≈0, 360822+j 0, 086905 A.

Соответствующая векторная диаграмма токов и напряжения (ВДТН) приведена на рисунке п4.2.2. Для удобства построения векторов на диаграмме вектор напряжения Ů совмещен с положительной вещественной полуосью Re комплексной плоскости.

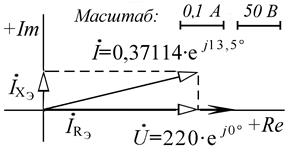
Рис. п4.2.2. Векторная диаграмма токов

и напряжения в схеме замещения параллельного типа

Пример № 4.3

Для двух потребителей, имеющих эквивалентные комплексные сопротивления Z_Э1 и Z_Э2, известны векторные диаграммы напряжения и тока (рис п4.3.1). Графоаналитическим методом определить активную и реактивную составляющую тока цепи при их параллельном соединении.

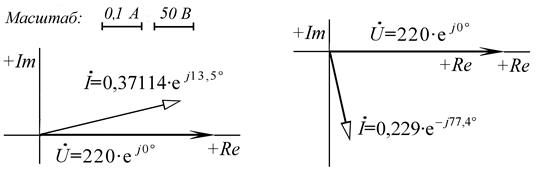
а) ВДТН для Z_Э1б) ВДТН для Z_Э2

Рис. п4.3.1. Векторные диаграммы потребителей

Решение

Вначале графоаналитически определим ток цепи при параллельном соединении потребителей (рис. п4.3.2а). Для нахождения его реактивной и активной составляющих измерим линейкой его проекции на вещественную и мнимую оси координат комплексной плоскости (рис. п4.3.2б). Как при построении исходных векторов, так и при определении полученных, используем соответствующие коэффициенты графического масштабирования.

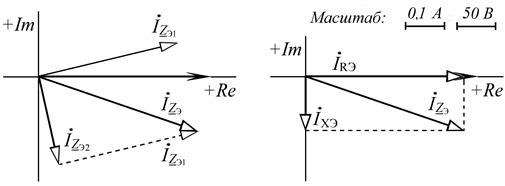
а) ВДТН суммы токов б) ВДТН составляющих тока

Рис. п4.3.2. Векторные диаграммы токов и напряжения

в схеме замещения параллельного типа

В результате графоаналитического определения токов в схеме замещения параллельного типа получим:

активная составляющая тока цепи

İ _R_Э ≈ 0,41 · e^j^0° А.

активная составляющая тока цепи

İ _X_Э ≈ 0,138 · e^–^j^90° А.

То, что фаза реактивной составляющей равна –90°, указывает на резистивно-индуктивный характер нагрузки цепи из двух параллельно включенных потребителей.

Пример № 5.1

В трехфазной четырехпроводной сети с нейтралью промышленной частоты (рис. п5.1.1) электрического освещения предприятия в качестве потолочных светильников используются люминесцентные светильники типа ПВЛП-1х40, а для местного освещения рабочих мест – настенные светильники типа НБ006-100 с лампами накаливания. Для включения светильников используются однополюсные автоматические выключатели, установленные в цеховом щитке ЩО рабочего освещения. Для компенсации реактивной энергии люминесцентных светильников установлена батарея конденсаторов C1, C2, СЗ.

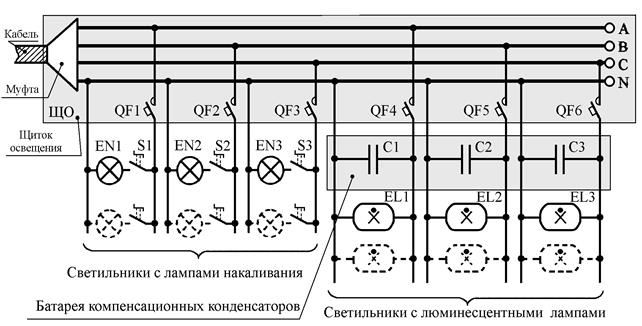Рис. п5.1.1. Принципиальная схема электрической сети освещения.

При условии симметричности нагрузки составить следующие схемы замещения:

а) осветительной нагрузки при включении всех светильников;

б) осветительной нагрузки при отсутствии ламп во всех светильниках;

в) осветительной нагрузки при отсутствии компенсирующих конденсаторов.

Решение

Схемы замещения (рис. п5.1.2) составляются с учетом того, что:

а) не учитывается наличие автоматических выключателей;

б) лампы накаливания являются чисто активной нагрузкой;

в) люминесцентные светильники являются активно-индуктивной нагрузкой;

г) компенсирующие конденсаторы являются чисто емкостной нагрузкой;

д) нагрузка во всех трех фазах полностью симметрична.

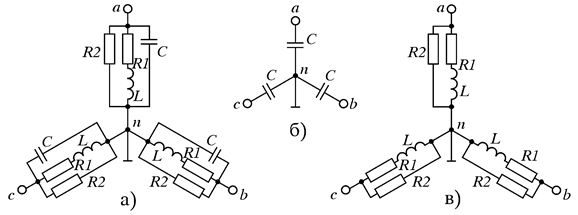
а - при включении всех светильников и компенсирующих конденсаторов;

б - при отсутствии ламп во всех светильниках;

в - при отсутствии компенсирующих конденсаторов

Рис. п5.1.2 - Схемы замещения трехфазной нагрузки

Пример № 5.2

Для одной фазы нагрузки сети электрического освещения предприятия (рис. п5.1.1) при отсутствии батареи компенсирующих конденсаторов рассчитать значение емкости компенсирующего конденсатора, при котором значение коэффициента мощности λ будет равно 0,85. Известны следующие параметры:

а) фазное напряжение - 127 В;

б) светильников с лампами накаливания по 60 Вт - 4 шт.;

в) люминесцентных светильников ПВЛП-1х80 - 10 шт.

Решение

Потребляемая светильниками с лампами накаливания активная мощность

P_EN_фазы = P_EN∙n_EN = 60∙4 = 240 Вт.

Потребляемая люминесцентными светильниками активная мощность

P_EL_фазы = P_EL∙n_EL = 80∙10 = 800 Вт.

Потребляемая всеми светильниками активная мощность

P_фазы = P_EN_фазы + P_EL_фазы = 240 + 800 = 1040 Вт.

Потребляемая люминесцентными светильниками реактивная мощность

Q_EL_фазы = P_EL (1 ⁄cosφ)² - 1 = 800 (1 ⁄0,47)² - 1 = 1 502,4 вар.

Полная мощность фазы

S_фазы = (P_EN_фазы + P_EL_фазы)² + Q²_E_L_фазы = (240 + 800)² + 1 502,4² = 1 702,1 BA.

Коэффициент мощности фазы без компенсирующего конденсатора

λ = (P_EN_фазы + P_EL_фазы) ⁄S_фазы = (240 + 800) ⁄1702,1 = 0,61 < 0,85.

При заданном значении λ в фазе реактивная мощность должна быть

Q_фазы = S_фазы·sinφ = S_фазы 1 - (cosφ)² = 1702,1 1 - 0,85² = 896,6 вар,

то есть, надо компенсировать конденсатором реактивную энергию

Q_С = Q_E_L_фазы - Q_фазы = 1502,4 - 896,6 = 605,8 вар.

Величина емкости компенсирующего конденсатора

C = 1 ⁄2πfx_C = Q_С ⁄2πfU²_ф_азы = 605,8 ⁄2π50·127² ≈ 0,00012 Ф = 120 мкФ.

Пример № 5.3

Для схем замещения (рис. п5.1.2а и п5.1.2б) вычислить токи в фазах и нейтральном проводе; активную, реактивную и полную мощность, а также построить векторные диаграммы токов и напряжений. Исходные значения параметров для расчетов взять из примера № 5.2.

Решение

Используя формулы из примеров № 5.1, № 5.2 и результаты расчетов из примера № 5.2, запишем энергетические параметры фаз схем замещения в таблицу п5.1.1. Соответствующие векторные диаграммы представлены на рисунке п5.3.1. Поскольку нагрузка является симметричной, то в таблице п5.3.1 приведены данные по каждой из трех схем замещения только для фазы "а".

Таблица п5.3.1

Схема	U_фазы, B	I_фазы, А	I_n, А	P_фазы, Вт	Q_фазы, вар	S_фазы, ВА	λ_фазы	φ, гр
Рис. 11.2,а		10,8			896,6	1373,1	0,85	+31,8
Рис. 11.2,б		4,77			605,8	605,8		-90

Активная мощность

P_фазы = 1040 Вт.

Реактивная мощность фазы без компенсирующего конденсатора

Q_фазы = 1502,4 вар.

Полная мощность фазы без компенсирующего конденсатора

S_фазы = 1702,1 ВА.

Ток фазы без компенсирующего конденсатора

I_фазы = S_фазы ∕ U_фазы = 1702,1 ∕ 127 = 13,4 А.

Угол сдвига фазы без компенсирующего конденсатора

φ_фазы = arc cos(P_фазы ∕ _Sфазы)= arc cos (1040 ∕ 1702,1) = +52,4°.

Реактивная мощность фазы с компенсирующим конденсатором

Q_фазы = 896,6 вар.

Полная мощность фазы с компенсирующим конденсатором

S_фазы = 1373,1ВА.

Ток фазы с компенсирующим конденсатором

I_фазы = 10,8 А.

Угол сдвига фазы с компенсирующим конденсатором

φ_фазы = +31,8°.

Реактивная и полная мощности фазы без ламп (P_фазы = 0 Вт)

S_фазы = Q_фазы = 896,6 вар.

Ток фазы с компенсирующим конденсатором

I_фазы = 10,8 А.

Угол сдвига фазы без ламп (P_фазы = 0 Вт)

φ_фазы = - 90°.

а) б)

Рис. п5.3.1. Векторные диаграммы напряжений и токов

симметричных потребителей.

Пример № 5.4

На щитке освещения ЩО цеха ателье (см. пример № 5.1) отключены автоматические выключатели QF1 и QF5. Параметры одной фазы нагрузки следующие:

а) фазное напряжение - 127 В;

б) светильников с лампами накаливания по 60 Вт - 4 шт.;

в) люминесцентных светильников ПВЛП-1х80 - 10 шт.;

г) коэффициент мощности с компенсирующим конденсатором - 0,85.

Необходимо составить схему замещения и вычислить токи в каждой фазе и построить векторную диаграмму, по которой определить ток в нейтральном проводе. Исходные значения параметров для расчетов взять из примера № 5.2.

Решение

Схема замещения представлена на рисунке п5.4.1а. Используя формулы и результаты расчетов из предыдущих примеров, рассчитаем энергетические параметры фаз схемы замещения, которые запишем в таблицу п5.4.1.

Векторная диаграмма токов и напряжений в фазах сети освещения цеха при отключенных автоматических выключателях QF1 и QF5 представлена на рисунке п5.4.2б.

Таблица п5.4.1.

Фаза	U_фазы, B	I_фазы, А	I_n, А	P_фазы, Вт	Q_фазы, вар	S_фазы, ВА	λ_фазы	φ, гр
"А"		9,46	~5,9		896,6	1201,6	0,67	+48,3
"B"		1,89
"C"		10,8		896,6	1373,1	0,85	+31,8

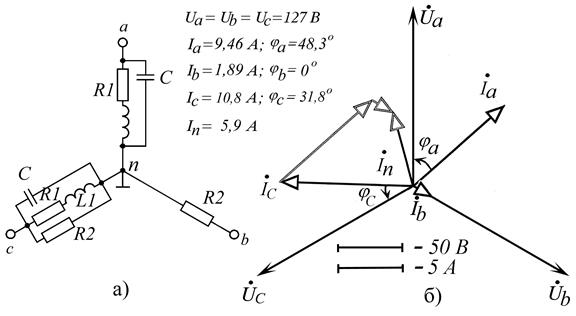
Рис. п5.4.1 - Схема замещения (а) и векторная диаграмма (б)

напряжений и токов трехфазной несимметричной нагрузки.

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Пример № 6.1

Для двух термисторов с параметрами статических характеристик К₁ = 0,97 Ом; К₂ = 1,46 Ом; β₁ = 2565 °К; β₂ = 2790 °К построить графики статических характеристик в интервале температур 250~400 °К, по которым определить величины сопротивлений этих термисторов при 0 °С и 100 °С. Для второго термистора определить ТКС при этих температурах.

Решение

Воспользуемся формулой статической характеристики термистора, на основании которой получим конкретные выражения для вычислений:

R_T = Ke^(β/^T⁾.

Для первого термистора

R₁_T = 0,97e⁽²⁵⁶⁵^/^T⁾.

Для второго термистора

R₂_T = 1,46e⁽²⁷⁹⁰^/^T⁾.

Результаты вычислений сведем в таблицу п6.1.1.

Таблица п6.1.1

<9 101112 13 14 15 >

Дата добавления: 2016-03-20; просмотров: 857;