Осмотическое давление растворов

Следствием закона Рауля является и то, что растворы обладают так называемым осмотическим давлением, изучаемым в курсе общей химии. Суть его такова.

1. а) Пусть два отсека в системе (рис. 8.5) разделены полупроницаемой мембраной, пропускающей только растворитель; причем в отсеке I находится чистый растворитель, а в отсеке II — раствор.

б) В соответствии со вторым началом термодинамики, система стремится выравнять концентрации веществ в отсеках. Поскольку путем перемещения растворенного вещества это невозможно сделать, то перемещается растворитель — из отсека I в отсек II.

в) Так вот, осмотическое давление раствора — это давление, которое надо приложить к раствору, чтобы воспрепятствовать перемещению вещества из отсека с чистым растворителем, отделенного полупроницаемой мембраной.

2. Осмотическое давление рассчитывают по формуле Вант-Гофера:

Как видно, оно равно тому газовому давлению, которым обладало бы растворенное вещество, если бы оно находилось в газообразном состоянии и занимало бы (при той же температуре) объем, равный объему раствора.

3. Вот основные моменты вывода этой формулы.

а) Можно убедиться, что избыточная энергия растворителя в отсеке II определяется отношением давлений его насыщенного пара над отсеками:

 

 

б) Энергия, создаваемая внешним давлением П, должна уравновешивать энергию растворителя:

 

в) С другой стороны, исходя из определения энергии Гиббса, можно доказать,
что в данном обратимом процессе (сдавливании раствора) изменение этой энергии определяется только изменением давления (так как объем практически не меняется):

где 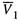— мольный объем чистого растворителя.

г) Приравнивая два выражения, получаем:

д) Переход же к формуле Вант-Гоффа (8.28) осуществляется так:

где V₀— объем раствора.

Первые три стадии этих выкладок — приближенные соотношения, спра-
ведливые лишь для разбавленных растворов.

8.9. Коллигативные свойства: общий перечень

1. В итоге, с законом Рауля связаны 4 явления, касающиеся влияния растворенного вещества на свойства раствора. Это

a) понижение давления насыщенного пара растворителя: ΔР₁/P⁰₁= Х₂, (8.17, в)

б) понижение температуры замерзания раствора: ΔТ_к = K_эб b₂ , (8.20)

в) повышение температуры кипения: ΔT_з = – К_з b₂, (8.21)

г) наличие осмотического давления: П ≈ с₂RT. (8.28)

2. Все эти явления объединяют в группу так называемых коллигативных свойств растворов.

а) Термин означает, что выраженность данных свойств зависит только от
количества частицрастворенного вещества в единице объема и не зависит от
их природы.

б) Однако такое утверждение (равно как и выписанные соотношения) спра-
ведливо только для идеальныхрастворов. В случае же неидеальныхрастворов
имеет значение и природа растворенного вещества.

Активности веществ

В вышеприведенных выражениях для коллигативных свойств растворов
фигурируют концентрации растворенных веществ. Использовались концентра-
ции и тогда, когда записывались формулы для константы равновесия, энергии
Гиббса химической реакции, химического потенциала, например:

1. а) Но на самом деле, как уже отмечалось для химического потенциала (6.9, б), во всех этих формулах следует писать не просто концентрации, а так называемые эффективные концентрации, или активностивеществ. Последние связаны с обычными концентрациями с помощью коэффициентов активности:

причем индексы (X, с, b) в обозначениях активности обычно не пишут. Так что под активностью иногда понимают эффективную молярную долю, в других случаях — эффективную молярную концентрацию, а в третьих — эффективную моляльную концентрацию.

б) С учетом сделанного замечания дадим определение. Активность вещества в растворе — это концентрация идеального раствора, которая требуется для проявления точно таких же коллигативных, химических и прочих свойств, как у данного реального раствора.

в) Следовательно, чтобы на практике определить коэффициент активности, необходимо измерить какое-либо свойство раствора, по соответствующей формуле рассчитать эффективную концентрацию и сравнить последнюю с истинной концентрацией.

3. При очень низких концентрациях вещества коэффициент активности близок к 1,0 (рис.8.6); при повышении концентрации он снижается (становясь много меньше 1,0); при еще большем увеличении концентрации начинает повышаться и порой даже становится больше 1,0. Некоторые значения коэффициента активности для СаСl₂ приведены в табл. 8.2.

4. Почему активность обычно отличается от концентрации?

Все дело во взаимодействии частиц вещества друг с другом. Например, ионы K⁺ и Cl^–, на которые распадается в растворе KCl, создают друг вокруг друга многочисленные ионные оболочки. Поэтому некоторая доля частиц как бы выключается из взаимодействия с растворителем и другими компонентами раствора.

5. Итак, в выражениях, где до сих пор писались концентрации, на самом деле
надо писать активности, например:

μ_i = μ⁰_i + RT ln (γ_i X_i) ,(8.35,а)

(a_C)^c (a_D)^d

ΔG_рц = ΔG⁰_рц + RT ln –––––––––– = ΔG⁰_рц + RT lnП_а .(8.35,б)

(a_A)^a (a_B)^b