Термодинамика растворения. Жидкие растворы
1. К аналогичному результату, как и для газовых растворов, нетрудно придти тогда, когда речь идет об образовании идеального жидкого раствора — например, при растворении твердого вещества (2) в жидкости (1).
а) Действительно, используя формулы (4.24) и (6.9, а) для химического потенциала, находим изменение энергии Гиббса какого-либо компонента:
ΔGi = ni Δμi = ni RT ln( Xi /1) , или ΔGi = ni RT ln Xi . (8.8, a-в)
Здесь учтено, что молярная доля компонента в чистом состоянии равна единице.
б) Конечная формула (8.8, в) совпадает с формулой для смешения газов (8.6,в).Следовательно, результирующее изменение энергии Гиббса вновь описывается формулами (8.7,а-б).
2. А если повысить концентрацию раствора с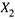 
до 
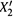путем растворения дополнительного количества вещества Δn2?
 |
а) Чтобы найти происходящее при этом изменение энергии Гиббса, надо
записать выражение (8.7, а) дважды — для исходного (
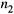) и для конечного ( 
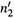)количества растворенного вещества, после чего вычесть первое выражение из второго. Результат таков:
б) I. Здесь первое слагаемое (относящееся к растворителю) — отрицательно (так как молярная доля растворителя уменьшается: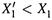 
).
II. Второе слагаемое относится к тому количеству растворенного вещества, которое изначально присутствовало в растворе. Его концентрация возрастает, так что данное слагаемое — положительно.
III. Третье же слагаемое вновь отрицательно.
3. Остановимся еще на одном аспекте.
а) Растворение вещества формально можно записать как обратимую химическую реакцию:
 |
где константа равновесия совпадает с молярной концентрацией насыщенного раствора:
 |
В соответствии с (4.34,а-б), уравнение изотермы такой «реакции» имеет вид:
б) Смысл вычисляемой по этим формулам энергии Гиббса заключается в следующем: согласно общему определению ΔGрц (п. 4.9), — это изменение энергии
Гиббса при растворении n2 молей вещества, если мольная доля последнего все
время остается на уровне X2 (а не снижается от 1 до X2, как предполагается
в формулах (8.8)).
Дата добавления: 2016-03-20; просмотров: 479;