Объект регулирования состоит из двух инерционных звеньев

(рис. 8.18).

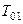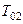Пусть регулируемый объект состоит из двух инерционных звеньев с постоянными времени и , причем 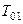- малая постоянная времени и 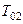- большая постоянная времени, которую нужно скомпенсировать регулятором. Постоянная времени 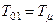является некомпенсируемой.

Для оптимизации контура необходимо включить регулятор с передаточной функцией 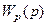последовательно с объектом и замкнуть обратной связью с коэффициентом .

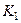Из условия оптимизации системы второго порядка следует, что замкнутая система второго порядка будет оптимизирована, если она обладает передаточной функцией

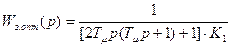. (8.30)

Передаточная функция разомкнутой оптимизированной системы имеет вид

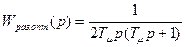. (8.31)

В то же время передаточная функция разомкнутой системы с учетом регулятора будет

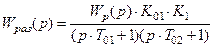. (8.32)

Приравнивая между собой выражения (8.31) и (8.32), получим требуемую передаточную функцию регулятора

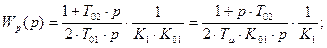(8.33)

или

,

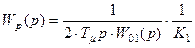где 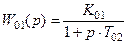- передаточная функция той части объекта регулирования, которая компенсируется данным регулятором;

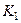- коэффициент обратной связи контура регулирования.