Принцип компенсации постоянных времени в системах подчиненного регулирования

Рассмотрим сущность компенсации постоянных времени для простейшего случая, когда объект регулирования представляет собой апериодическое звено. Такие звенья чаще всего входят в состав объекта регулирования. При больших значениях постоянных времени они могут существенно влиять на быстродействие системы регулирования. Передаточная функция такого звена

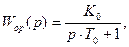
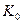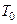где и - соответственно коэффициент усиления и постоянная времени звена.

Очевидно, что для осуществления абсолютной компенсации постоянной времени и превращения инерционного звена в усилительное, необходимо последовательно с объектом включить регулятор с передаточной функцией дифференцирующего звена (рис.8.16)

,

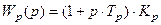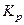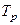где и - соответственно коэффициент усиления и постоянная времени регулятора.

В этом случае при 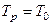имеем

.

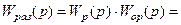
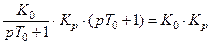Физически это означает, что для мгновенного изменения выходной величины инерционного звена, нужно подать на его вход импульс напряжения бесконечной амплитуды (мгновенное форсирование).

Поэтому в реальных системах, имеющих ограниченные ресурсы управления, абсолютная компенсация неосуществима. Тем не менее, если применяется безынерционный регулятор, то при малых задаваемых приращениях выходной величины объекта принципиально-возможная степень компенсации приближается к абсолютной. Однако, при такой степени компенсации контур регулирования становится весьма чувствительным к помехам.

Поэтому для инерционного звена объекта регулирования степень приближения компенсации к абсолютной ограничивается пределом, при котором полоса пропускания замкнутого контура обеспечивает его помехозащищенность. Последнее условие, в частности, может быть удовлетворено применением ПИ-регулятора с передаточной функцией

.

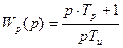Если 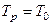, то передаточная функция разомкнутого контура будет иметь вид

.

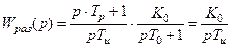Это соответствует передаточной функции интегрального звена с постоянной времени интегрирования 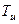. При замыкании контура единичной обратной (рис. 3.16) связью, получим

.

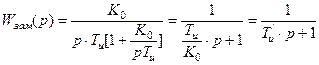Статическая ошибка такого замкнутого контура сводится к нулю из-за наличия интегрирующего звена в разомкнутой части системы. Следовательно, результатом компенсации явилась замена в разомкнутом контуре апериодического звена с большой постоянной времени 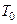интегрирующим звеном и постоянной времени 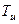в разомкнутой системе и инерционным звеном с малой постоянной времени 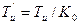в замкнутом состоянии.

Данный принцип компенсации используется при построении систем подчиненного регулирования.