Логарифмические частотные характеристики разомкнутых оптимальных систем

Для оптимальной системы второго порядка ( 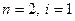) можно записать следующие выражения для передаточной функции и частотных характеристик:

,

,

,

.

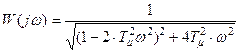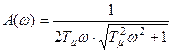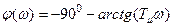ЛАЧХ и ЛФЧХ разомкнутых оптимальных систем могут быть построены исходя из передаточных функций разомкнутых систем. Так для системы второго порядка (n=2) с передаточной функцией

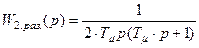
имеем два последовательно соединенных звена:

1) апериодического звена с передаточной функцией

,

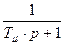где 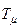- суммарная величина малых постоянных времени, которые не могут быть скомпенсированы регулятором;

2) интегрирующего звена с передаточной функцией

.

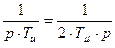На рис. 8.12. построены ЛАЧХ и ЛФЧХ разомкнутой системы, настроенной по модульному оптимуму.

Логарифмические амплитудные частотные характеристики могут быть построены с учетом выражения

,

.

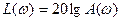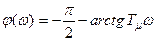На рис.8.12. представлены логарифмические частотные характеристики 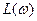и для оптимальной системы второго порядка. Запас по фазе такой системы составляет

.

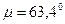При повышении порядка САР уменьшается частота среза. Однако запас по фазе практически не меняется.

Для замкнутой системы

.

Здесь: - частота среза;

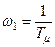- частота сопряжения асимптот ЛАЧХ;

- запас по фазе при частоте среза .

Важнейшие достоинства рассматриваемого метода оптимизации является его простота и определенность получаемых статических и динамических качеств контура регулирования. Однако последнее одновременно может явиться и недостатком, т.к. требования к точности регулирования в ряде случаев могут быть более высокими, чем к точности, соответствующей модульному оптимуму. Поэтому кроме настройки на технический оптимум используют настройку по т.н. симметричному оптимуму, рассмотренному ниже.