Переходные функции оптимальных САР
Переходные функции оптимальных САР зависят от порядка объекта регулирования и номера контура регулирования
1) 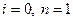
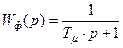 ;
; 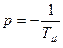 ;
; 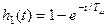 ,
,

т.е. переходный процесс соответствует апериодическому звену первого порядка (рис. 8.7).
2) 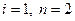
Характеристическое уравнение
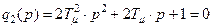 (8.22)
(8.22)
или 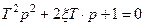 ,
,
где 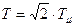 ,
, 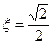 .
.
Корни характеристического уравнения
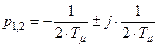 .
.
При ступенчатом воздействии на вход оптимальной системы второго порядка переходный процесс будет описываться следующим уравнением
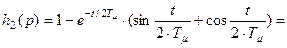
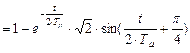 . (8.23)
. (8.23)
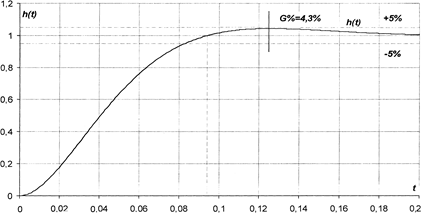
Кривая переходного процесса представлена на рис.8.8.
|
Переходная функция характеризуется следующими показателями:
 = 4,3 % - перерегулирование;
= 4,3 % - перерегулирование;
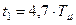 - время первого достижения установившегося значения;
- время первого достижения установившегося значения;
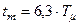 - время достижения максимума;
- время достижения максимума;
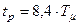 - время переходного процесса (вхождение в 2% зону ошибки).
- время переходного процесса (вхождение в 2% зону ошибки).
Быстродействие контура определяется временем  , соответствующим моменту, когда регулируемая величина первый раз достигает установившегося значения. Из кривых (рис.8.9) видно, что при снижении
, соответствующим моменту, когда регулируемая величина первый раз достигает установившегося значения. Из кривых (рис.8.9) видно, что при снижении 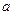 возрастает колебательность процесса и его перерегулирование. Выбирая коэффициент
возрастает колебательность процесса и его перерегулирование. Выбирая коэффициент 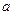 в пределах
в пределах 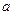 =1 ¸ 4 можно получить любой желаемый переходный процесс с заданными оптимальными показателями. Поэтому рассмотренный метод коррекции называют методом оптимизации контура регулирования по быстродействию. Такая настройка контура регулирования (системы второго порядка) не является предельной ни по быстродействию (время
=1 ¸ 4 можно получить любой желаемый переходный процесс с заданными оптимальными показателями. Поэтому рассмотренный метод коррекции называют методом оптимизации контура регулирования по быстродействию. Такая настройка контура регулирования (системы второго порядка) не является предельной ни по быстродействию (время  можно уменьшить, уменьшая
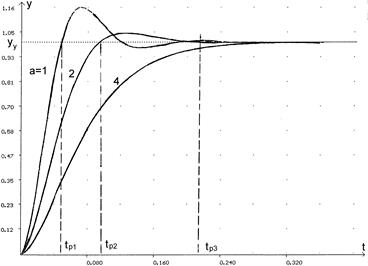
можно уменьшить, уменьшая 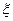 ), ни по перерегулированию, которое можно уменьшить либо вообще исключить ценой снижения быстродействия. Однако, в большинстве технических случаев она удовлетворяет практическим требованиям. Благодаря простоте реализации оптимизация по модульному оптимуму стала наиболее распространенным методом оптимальной настройки систем регулирования.
), ни по перерегулированию, которое можно уменьшить либо вообще исключить ценой снижения быстродействия. Однако, в большинстве технических случаев она удовлетворяет практическим требованиям. Благодаря простоте реализации оптимизация по модульному оптимуму стала наиболее распространенным методом оптимальной настройки систем регулирования.
|
3) 
Характеристическое уравнение имеет вид
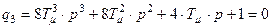 .
.
Корни характеристического уравнения
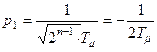 ;
; 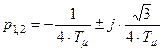 .
.
Дата добавления: 2016-03-20; просмотров: 1194;