Оптимальные передаточные функции САР

Рассмотренные выше соображения позволяют определить передаточные функции разомкнутых и замкнутых контуров регулирования при любом порядке объекта регулирования. Обозначим:

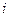- номер контура регулирования;

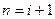- порядок объекта регулирования.

В этом случае получим для передаточных функций оптимальных разомкнутого и замкнутого контуров следующие выражения:

,

.

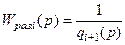В зависимости от порядка регулирования имеем:

1) ,

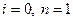
т.е. имеем объект с передаточной функцией инерционного звена первого порядка – фильтр.

2) 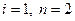(первый контур регулирования, объект регулирования второго порядка)

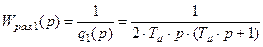. (8.13)

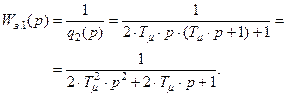(8.14)

3) (второй контур регулирования, объект регулирования третьего порядка)

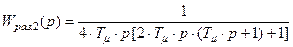; (8.15)

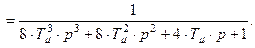(8.16)

4) 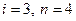(третий контур регулирования, объект регулирования четвертого порядка)

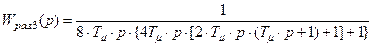; (8.17)

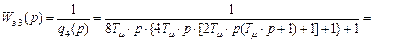
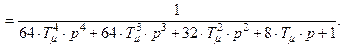(8.18)

Аналогично можно записать выражения передаточных функций для систем более высокого порядка.

Можно показать, что при 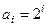внутренний по отношению к рассматриваемому контур (колебательное звено) может быть представлен апериодическим звеном с периодической функцией

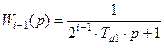. (8.19)

В этом случае для 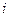-го контура регулирования можно записать при стандартной настройке, т.е. при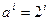

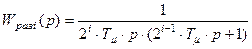, (8.20)

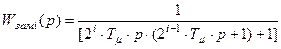. (8.21)

Следовательно, с увеличением номера контура регулирования постоянная времени, не компенсируемая регулятором, возрастает в раз по сравнению с этой постоянной времени 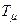для первого контура. В результате быстродействие контура снижается в 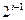раз ( ).