Критерии качества оптимального регулирования
Оптимальная САР должна соответствовать конкретному критерию качества регулирования, на основании которого она построена.
За критерий качества процессов в системе можно принимать следующие интегралы:
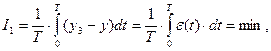
(8.1)
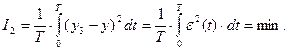
Следовательно, за критерий оптимальности принимается минимум либо линейного, либо квадратичного отклонения выходной величины 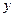 от заданного значения
от заданного значения
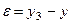 .
.
Интегральный критерий 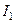 применим только в системах, о которых заведомо известно, что у них переходные процессы монотонны, т.е.
применим только в системах, о которых заведомо известно, что у них переходные процессы монотонны, т.е.  не меняет знака (рис.8.3, кривая 1).
не меняет знака (рис.8.3, кривая 1).

Это резко ограничивает возможности данного критерия. Если переходный процесс колебательный, то величина 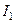 не может служить мерой его качества, т.к. величина
не может служить мерой его качества, т.к. величина 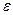 имеет разный знак (рис.8.4), т.е. площади, ограничиваемые кривой
имеет разный знак (рис.8.4), т.е. площади, ограничиваемые кривой 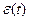 будут вычитаться друг из друга. При линейной оптимизации получается увеличенное время регулирования (кривая 1).
будут вычитаться друг из друга. При линейной оптимизации получается увеличенное время регулирования (кривая 1).
|

 |
Интегральный критерий
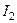 обеспечивает минимум квадратичной ошибки регулирования. Неограниченное снижение
обеспечивает минимум квадратичной ошибки регулирования. Неограниченное снижение 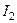 невозможно из-за возможных ограничений в системе регулирования. При квадратичном критерии получается большая величина перерегулирования.
невозможно из-за возможных ограничений в системе регулирования. При квадратичном критерии получается большая величина перерегулирования.
При линейной и квадратичной оптимизации могут быть получены либо слишком сильно, либо слишком слабо задемпфированные процессы. Для того, чтобы получить переходный процесс без чрезмерного перерегулирования и с минимальным временем необходим некоторый технический оптимум. В соответствии с этим оптимумом за оптимальный процесс принимается такой, при котором перерегулирование составляет  £ 5 %, а время регулирования наименьшее возможное. Такой реакцией на скачок входной задающей величины обладают системы второго порядка с коэффициентом демпфирования
£ 5 %, а время регулирования наименьшее возможное. Такой реакцией на скачок входной задающей величины обладают системы второго порядка с коэффициентом демпфирования 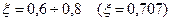 .
.
Изменение соотношения постоянных времени может быть достигнуто применением параллельной или последовательной коррекции. В системах с параллельной коррекцией применяются гибкие отрицательные обратные связи, с помощью которых увеличивается наибольшая постоянная времени и уменьшаются остальные. В результате достигается возможность использования повышенных значений коэффициента форсировки, что приводит к повышению быстродействия переходного процесса.
Основным недостатком систем с параллельной коррекцией является сложность расчета оптимальных параметров системы, трудность настройки и наладки систем управления.
В системах с последовательной коррекцией корректирующие звенья включают в цепь основного сигнала последовательно со звеньями систем управления. К системам с последовательной коррекцией относятся так называемые системы подчиненного регулирования. В этих системах требуемые соотношения постоянных времени могут быть достигнуты заменой (компенсацией) с помощью регуляторов всех больших постоянных времени, кроме одной, самой малой, новыми постоянными, кратными самой малой постоянной времени.
Рассмотрим, какие соотношения постоянных времени должны быть обеспечены для получения оптимальных по времени переходных процессов.
Рассмотрим вначале простую замкнутую систему, состоящую из одного интегрирующего и одного инерционного звеньев (рис.8.5) с единичной обратной связью, причем Т1 < Т2.

Передаточная функция такой замкнутой системы
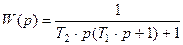 . (8.2)
. (8.2)
Уравнение амплитудной частотной характеристики в этом случае будет
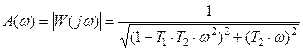 , (8.3)
, (8.3)
или
 . (8.4)
. (8.4)
Ранее в курсе ТАУ было показано, что при скачкообразном изменении входного сигнала регулируемая величина будет тем точнее следовать за заданной величиной, чем шире полоса частот, при которых модуль передаточной функции приближен к единице (рис.8.6).

Чем ближе к единице модуль передаточной функции, тем меньше динамическая ошибка регулирования и меньше время переходного процесса.
Для нашего случая 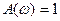 , если
, если
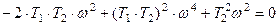 .
.
Можно показать, что этому равенству соответствует соотношение 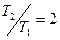 , т.е.
, т.е. 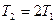 .
.
И.Кесслером (фирма SIEMENS) такой критерий был назван «Betragsoptimum». В нашей практике его называют «техническим» или «модульным оптимумом» (наиболее удачное название).
Если обозначить наименьшую постоянную времени системы через 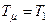 , то передаточная функция замкнутой оптимальной системы (8.2) запишется
, то передаточная функция замкнутой оптимальной системы (8.2) запишется
 (8.5)
(8.5)
где 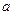 - коэффициент, определяющий соотношение постоянных времени в системе регулирования;
- коэффициент, определяющий соотношение постоянных времени в системе регулирования;
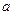 =2 – стандартный коэффициент, соответствующий «модульному оптимуму» (оптимальная настройка);
=2 – стандартный коэффициент, соответствующий «модульному оптимуму» (оптимальная настройка);
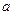 = 1 ¸ 4 – реальный коэффициент настройки для реальных систем.
= 1 ¸ 4 – реальный коэффициент настройки для реальных систем.
Дата добавления: 2016-03-20; просмотров: 928;
