ГЛАВА 3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
В главе введены понятия относительного, переносного и абсолютного движений точки, кориолисова ускорения, изложена методика определения скоростей и ускорений точки в сложном движении.
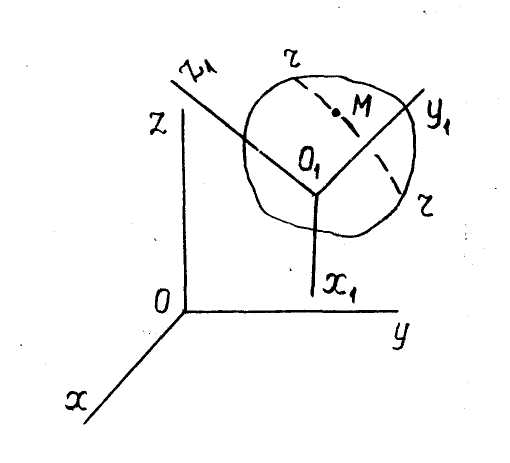
| Рис.35 |
 движется по некоторой траектории
движется по некоторой траектории 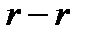 относительно тела
относительно тела 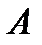 , которое, в свою очередь, движется относительно условно неподвижной системы осей
, которое, в свою очередь, движется относительно условно неподвижной системы осей 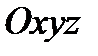 , обычно связанных с Землёй (рис. 35). Для изучения движения точки
, обычно связанных с Землёй (рис. 35). Для изучения движения точки 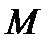 относительно тела
относительно тела 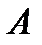 вводим подвижную систему осей
вводим подвижную систему осей 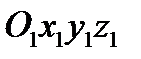 , связанную с телом. Движение точки
, связанную с телом. Движение точки  относительно подвижной системы отсчёта называют относительным движением точки.
относительно подвижной системы отсчёта называют относительным движением точки.
Скорость 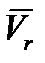 и ускорение
и ускорение 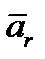 точки
точки  в относительном движении называют относительной скоростью и относительным ускорением. Движение подвижной системы отсчёта
в относительном движении называют относительной скоростью и относительным ускорением. Движение подвижной системы отсчёта 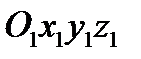 и неизменно связанного с ней тела
и неизменно связанного с ней тела 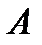 по отношению к неподвижной системе отсчёта
по отношению к неподвижной системе отсчёта 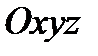 является для точки
является для точки  переносным движением.
переносным движением.
Скорость 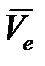 и ускорение
и ускорение 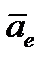 той точки тела
той точки тела 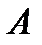 , где в данный момент времени находится точка
, где в данный момент времени находится точка  , называют переносной скоростью и переносным ускорением точки
, называют переносной скоростью и переносным ускорением точки  .
.
Движение точки  относительно неподвижной системы отсчётаназывают абсолютным движением точки.
относительно неподвижной системы отсчётаназывают абсолютным движением точки.
Скорость 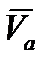 и ускорение
и ускорение 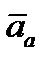 точки
точки  в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки.
в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки.
Согласно теореме о сложении скоростей, абсолютная скорость точки 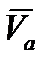 равна геометрической сумме её переносной скорости
равна геометрической сумме её переносной скорости 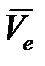 и относительной скорости
и относительной скорости 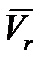
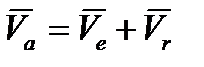 . (3.1)
. (3.1)
По теореме Кориолиса о сложении ускорений абсолютное ускорение точки 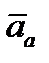 равно геометрической сумме переносного
равно геометрической сумме переносного 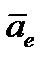 , относительного
, относительного  и кориолисова
и кориолисова 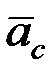 ускорений
ускорений
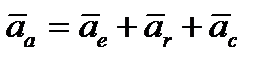 . (3.2)
. (3.2)
Кориолисово ускорение 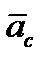 равно удвоенному векторному произведению угловой скорости
равно удвоенному векторному произведению угловой скорости 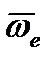 переносного движения на относительную скорость точки
переносного движения на относительную скорость точки 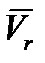
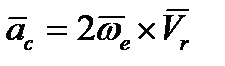 . (3.3)
. (3.3)
Векторное равенство определяет модуль ускорения Кориолиса
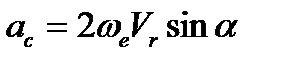 , (3.4)
, (3.4)
где 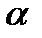 – меньший угол между векторами
– меньший угол между векторами  и
и 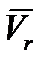 и его направление (рис. 36).
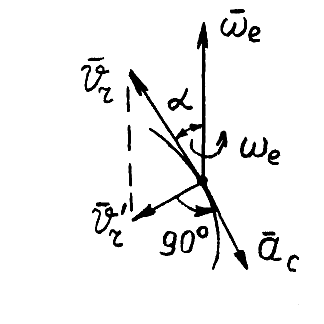
и его направление (рис. 36).
| Рис. 36 |
| Относительная траектория |
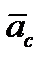 направлено перпендикулярно плоскости, образованной векторами
направлено перпендикулярно плоскости, образованной векторами 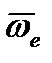 и
и 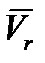 , в ту сторону, откуда поворот от вектора
, в ту сторону, откуда поворот от вектора 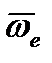 к вектору
к вектору 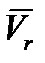 на угол
на угол 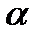 представляется происходящим против хода часовой стрелки.
представляется происходящим против хода часовой стрелки.
Для определения направления ускорения Кориолиса 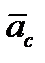 удобно пользоваться правилом Жуковского: проецируем вектор относительной скорости
удобно пользоваться правилом Жуковского: проецируем вектор относительной скорости 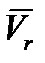 на плоскость, перпендикулярную вектору
на плоскость, перпендикулярную вектору 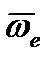 , далее поворачиваем полученную проекцию
, далее поворачиваем полученную проекцию 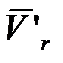 на угол 90° в направлении вращения переносной угловой скорости
на угол 90° в направлении вращения переносной угловой скорости 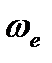 , получаем направление кориолисова ускорения
, получаем направление кориолисова ускорения 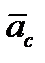 .
.
Из выражений (3.4) вытекают условия, при выполнении которых ускорение Кориолиса равно 0.
Очевидно, 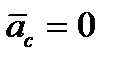 , если:
, если:
1) 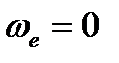 ; учитывая, что
; учитывая, что 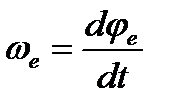 , где
, где 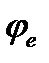 – угол поворота тела
– угол поворота тела 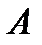 , движение которого для точки
, движение которого для точки  является переносным (рис. 36). Производная
является переносным (рис. 36). Производная 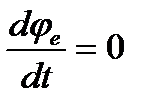 в двух случаях: а)
в двух случаях: а) 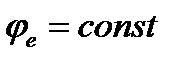 , то есть переносное движение является поступательным; б)
, то есть переносное движение является поступательным; б) 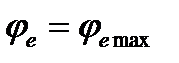 и
и 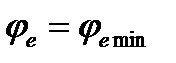 , угол поворота тела
, угол поворота тела 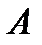 имеет экстремальное значение (в моменты времени изменения направления переносной угловой скорости
имеет экстремальное значение (в моменты времени изменения направления переносной угловой скорости 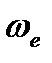 );
);
2) 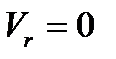 ; так как
; так как 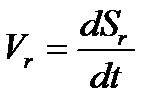 , где
, где 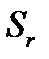 – дуговая координата в относительном движении точки
– дуговая координата в относительном движении точки  , то
, то 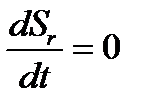 также в двух случаях: а)
также в двух случаях: а) 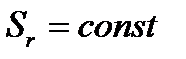 (нет относительного движения точки); б)
(нет относительного движения точки); б) 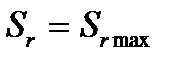 и
и 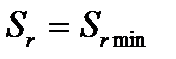 (моменты изменения направления относительного движения точки);
(моменты изменения направления относительного движения точки);
3) 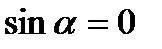 ; значит,
; значит, 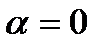 , либо
, либо 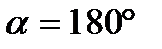 , то есть это случай, когда векторы
, то есть это случай, когда векторы 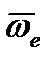 и
и 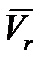 параллельны.
параллельны.
Рассмотрим характерные примеры решения задач на сложное движение точки.
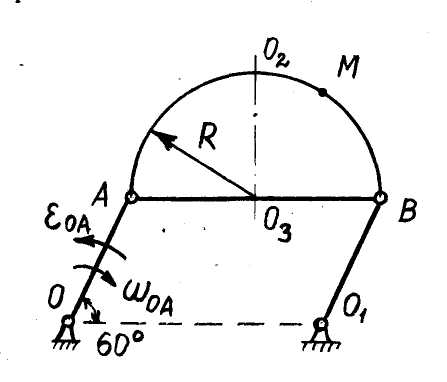
| Рис.37 |
 (рис. 37) движется по жёлобу радиусом
(рис. 37) движется по жёлобу радиусом 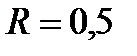 м звена АВ механизма шарнирного четырёхзвенника
м звена АВ механизма шарнирного четырёхзвенника 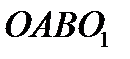 по закону
по закону  ,
, 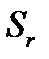 – в м. Заданное положение механизма соответствует моменту времени
– в м. Заданное положение механизма соответствует моменту времени 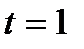 с, и в этом положении угловая скорость и угловое ускорение кривошипа
с, и в этом положении угловая скорость и угловое ускорение кривошипа 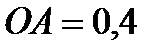 мравны
мравны 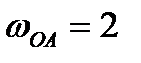 рад/с,
рад/с, 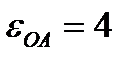 рад/с². Определить абсолютные скорость и ускорение точки
рад/с². Определить абсолютные скорость и ускорение точки  в данный момент времени, если
в данный момент времени, если 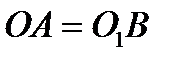 и
и 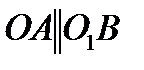 .
.
Решение задач на сложное движение точки надо начинать с установления её относительного движения, далее найти переносное и наконец абсолютное движение. В некоторых задачах, к которым относится и данный пример, это можно сделать сразу без дополнительных исследований. Подробно определение движений приведено в примере 3. В рассматриваемом примере движение точки  по звену
по звену 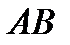 – движение относительное, движение звена
– движение относительное, движение звена 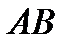 – переносное движение для точки
– переносное движение для точки  , сумма относительного и переносного движений даёт абсолютное движение точки.
, сумма относительного и переносного движений даёт абсолютное движение точки.
Находим положение точки  на звене
на звене 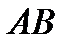 в заданный момент времени
в заданный момент времени 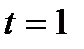 с
с
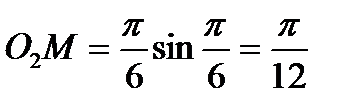 м, тогда
м, тогда 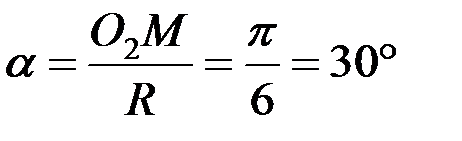 (рис. 38).
(рис. 38).
Абсолютная скорость точки равна
 . (3.5)
. (3.5)
Переносная скорость 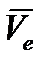 равна скорости той точки звена
равна скорости той точки звена 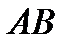 , где находится точка
, где находится точка  в данный момент времени. Так как в рассматриваемой задаче дано, что
в данный момент времени. Так как в рассматриваемой задаче дано, что 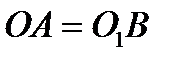 и
и 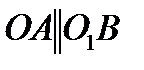 , то звено
, то звено 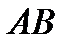 четырёхзвенника движется поступательно. Значит, согласно основной теореме поступательного движения тела
четырёхзвенника движется поступательно. Значит, согласно основной теореме поступательного движения тела 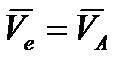 ,
,
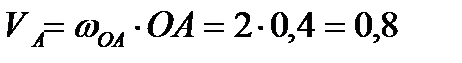 м/с.
м/с.
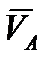 направлена
направлена 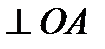 в сторону вращения
в сторону вращения 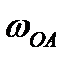 . Для угла
. Для угла 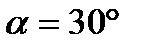 скорость
скорость 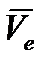 направлена перпендикулярно радиусу
направлена перпендикулярно радиусу 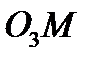 траектории относительного движения точки.
траектории относительного движения точки.
Относительная скорость точки равна
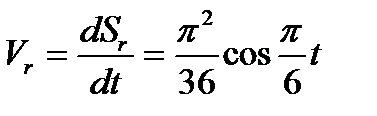 .
.
При 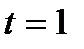 с
с 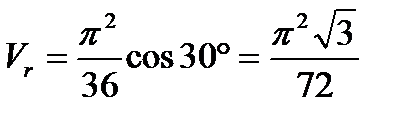 м/с.
м/с.
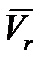 направлена по касательной к траектории относительного движения, то есть в заданном положении точки скорости
направлена по касательной к траектории относительного движения, то есть в заданном положении точки скорости 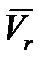 и
и 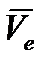 направлены по одной линии (рис. 38). Поэтому для заданного положения точки абсолютная скорость
направлены по одной линии (рис. 38). Поэтому для заданного положения точки абсолютная скорость
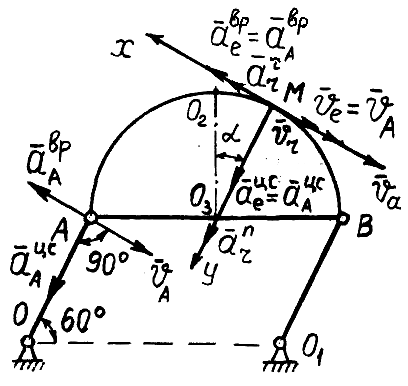
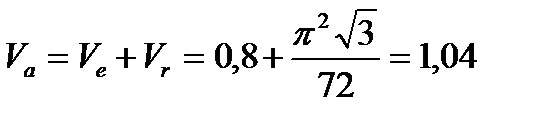 м/с.
м/с.
Абсолютное ускорение точки равно
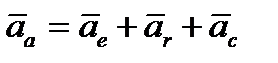 . (3.6)
. (3.6)
Переносное ускорение
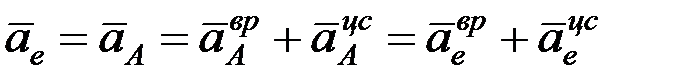 .
.
Так как относительное движение точки криволинейное, то относительное ускорение равно
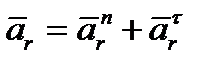 .
.
Тогда
| Рис.38 |
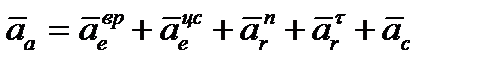 . (3.7)
. (3.7)
Находим модули и направляем составляющие абсолютного ускорения 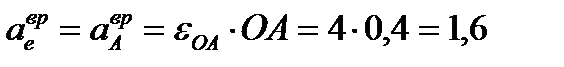 м/с²;
м/с²; 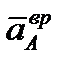 направлен
направлен 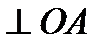 в сторону
в сторону 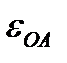 .
.
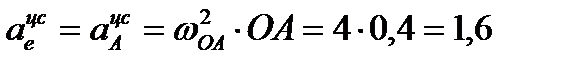 м/с²;
м/с²; 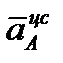 направлен по
направлен по 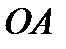 от
от 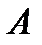 к
к  .
.
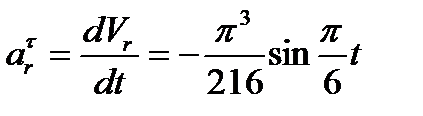 ; при
; при 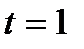 с
с 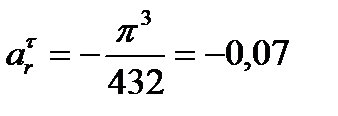 м/с².
м/с².
Знак «минус» в 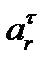 показывает, что вектор
показывает, что вектор 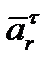 направлен в сторону уменьшения дуговой координаты
направлен в сторону уменьшения дуговой координаты 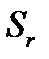 . Далее
. Далее 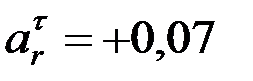 м/с².
м/с².
 м/с².
м/с².
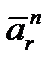 направлен по
направлен по 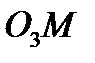 к центру
к центру 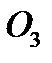 (рис. 38).
(рис. 38).
Ускорение Кориолиса
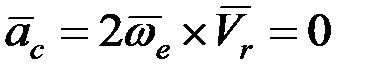 ,
,
так как звено 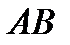 движется поступательно, то
движется поступательно, то 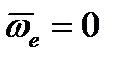 .
.
Поскольку все векторы составляющих абсолютного ускорения в рассматриваемом примере расположены в плоскости чертежа, для определения его модуля выбираем две любые перпендикулярные оси, например 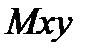 ,и находим две проекции абсолютного ускорения на эти оси:
,и находим две проекции абсолютного ускорения на эти оси:
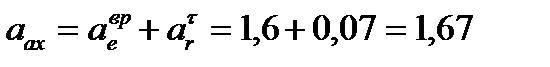 м/с²,
м/с²,
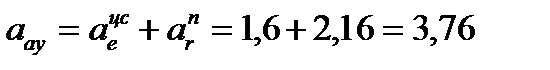 м/с².
м/с².
Тогда
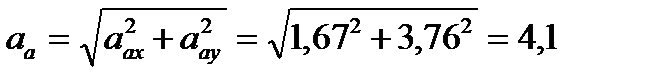 м/с².
м/с².
Пример 2. Точка  движется с постоянной скоростью
движется с постоянной скоростью 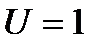 м/с по жёлобу
м/с по жёлобу 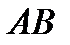 квадратной пластины со стороной
квадратной пластины со стороной 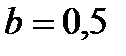 м от
м от 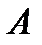 к
к 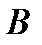 . Пластина вращается вокруг оси
. Пластина вращается вокруг оси 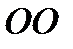 ускоренно. В данный момент времени угловая скорость
ускоренно. В данный момент времени угловая скорость  рад/с, угловое ускорение
рад/с, угловое ускорение 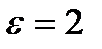 рад/с² и точка
рад/с² и точка  занимает на пластине положение, указанное на рис. 39. Определить абсолютную скорость и абсолютное ускорение точки.
занимает на пластине положение, указанное на рис. 39. Определить абсолютную скорость и абсолютное ускорение точки.
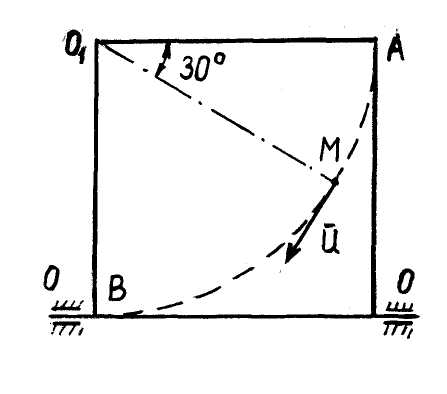 Для решения задачи зададим направление
Для решения задачи зададим направление 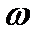 и
и 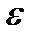 . Абсолютная скорость точки
. Абсолютная скорость точки  равна
равна
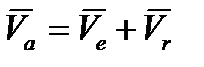 . (3.8)
. (3.8)
Относительная скорость 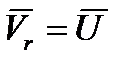 . Вектор
. Вектор 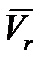 направлен по касательной к траектории относительного движения точки (рис. 40).
направлен по касательной к траектории относительного движения точки (рис. 40).
Переносная скорость
| Рис. 39 |
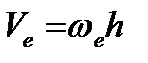 ,
,
где 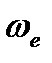 – угловая скорость движения пластины (
– угловая скорость движения пластины ( 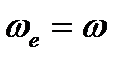 ),
), 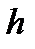 – радиус вращения той точки пластины, где находится точка М в данный момент времени.
– радиус вращения той точки пластины, где находится точка М в данный момент времени.
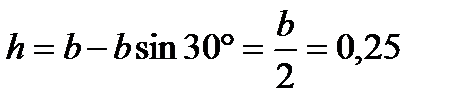 м.
м.
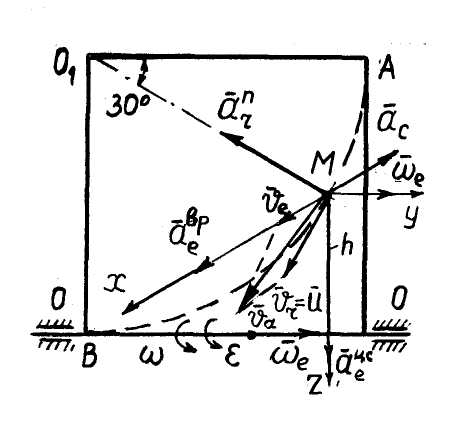
| Рис. 40 |
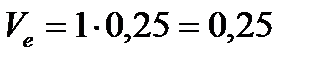 м/с.Вектор
м/с.Вектор 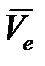 направлен на нас. Так как в данном примере
направлен на нас. Так как в данном примере 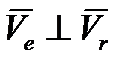 , то
, то
| м/с. |
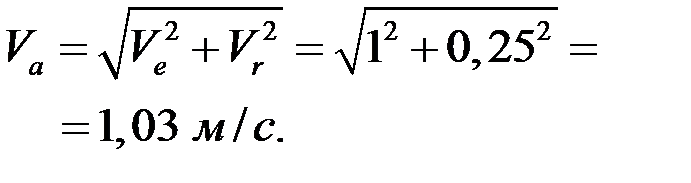
Абсолютное ускорение точки равно
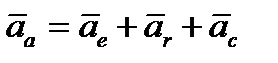 . (3.9)
. (3.9)
Так как переносное движение – вращательное, а относительное – криволинейное, то имеем
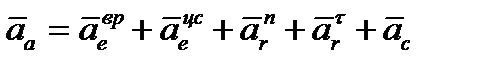 . (3.10)
. (3.10)
Переносное вращательное ускорение равно
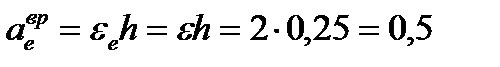 м/с².
м/с².
Вектор  направлен на нас.
направлен на нас.
Переносное центростремительное ускорение равно
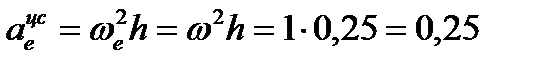 м/с².
м/с².
Вектор 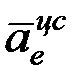 направлен вниз.
направлен вниз.
Касательное ускорение
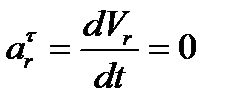 ,
,
так как по условию задачи 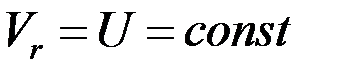 .
.
Нормальное ускорение
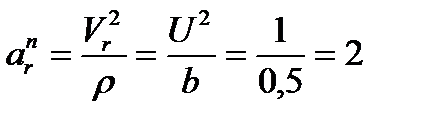 м/с².
м/с².
Вектор 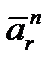 направлен к центру кривизны траектории относительного движения, то есть к O1.
направлен к центру кривизны траектории относительного движения, то есть к O1.
Ускорение Кориолиса  . Вектор
. Вектор 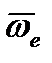 направлен по оси OO, и его направление можно найти, используя правило буравчика.
направлен по оси OO, и его направление можно найти, используя правило буравчика.
Переносим вектор 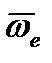 в точку
в точку  . Тогда меньший угол между векторами
. Тогда меньший угол между векторами  и
и 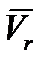 равен 120º. Значит
равен 120º. Значит
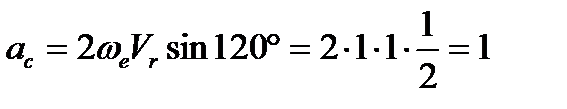 м/с².
м/с².
Используя правило векторного произведения или правило Жуковского, находим, что вектор 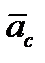 направлен в противоположную от нас сторону (против
направлен в противоположную от нас сторону (против  ) (рис. 40).
) (рис. 40).
Выбираем систему перпендикулярных осей 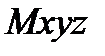 и находим три проекции абсолютного ускорения на выбранные оси:
и находим три проекции абсолютного ускорения на выбранные оси:
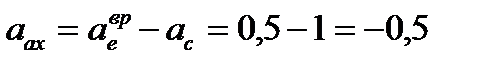 м/с²;
м/с²;
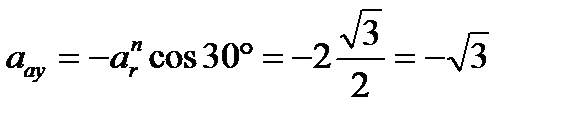 м/с²;
м/с²;
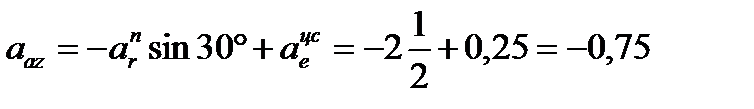 м/с².
м/с².
Тогда абсолютное ускорение точки равно
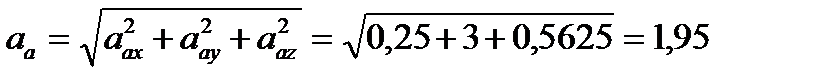 м/с².
м/с².
| x1 |
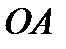 вращается вокруг оси O с угловой скоростью
вращается вокруг оси O с угловой скоростью  рад/с, угловым ускорением
рад/с, угловым ускорением 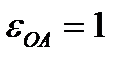 рад/с² и приводит в движение кулису
рад/с² и приводит в движение кулису 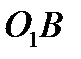 , вращающуюся вокруг оси
, вращающуюся вокруг оси 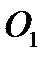 .
.
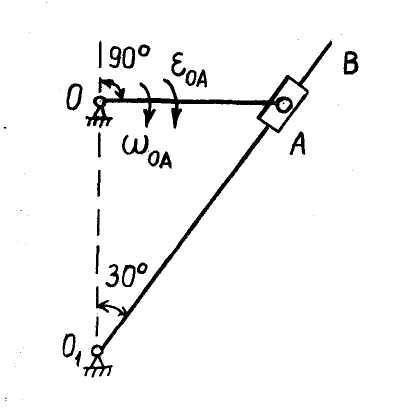 Считая вращение кривошипа ускоренным, определить в заданном положении механизма угловую скорость и угловое ускорение кулисы
Считая вращение кривошипа ускоренным, определить в заданном положении механизма угловую скорость и угловое ускорение кулисы 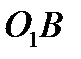 , если OA = 4 м,
, если OA = 4 м, 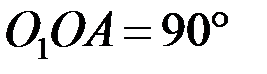 ,
, 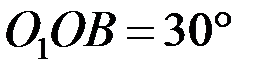 .
.
| y1 |
| Рис.41 |
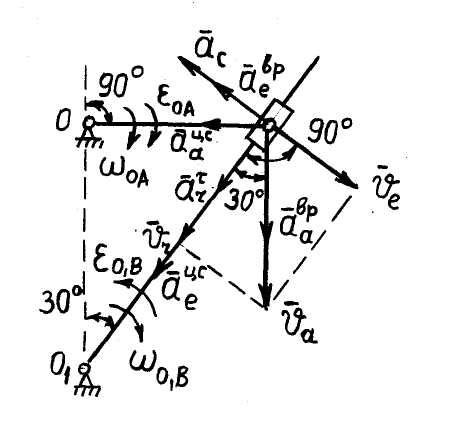
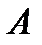 совершает сложное движение: точка
совершает сложное движение: точка 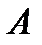 кривошипа ОА вращается вместе с ним вокруг оси О; точка А кулисы
кривошипа ОА вращается вместе с ним вокруг оси О; точка А кулисы 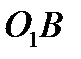 , вращается вместе с ней вокруг оси
, вращается вместе с ней вокруг оси 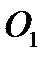 ; точка
; точка 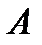 ползуна движется вместе с ним по кулисе.
ползуна движется вместе с ним по кулисе.
| Рис.42 |
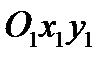 , связанную с кулисой
, связанную с кулисой 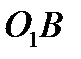 . Поскольку расстояние
. Поскольку расстояние 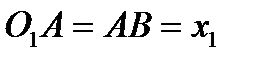 меняется при вращении кривошипа
меняется при вращении кривошипа 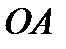 , то, согласно определению относительного движения, движение ползуна
, то, согласно определению относительного движения, движение ползуна 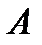 по кулисе
по кулисе 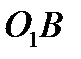 есть движение относительное. Тогда вращение кулисы
есть движение относительное. Тогда вращение кулисы  – движение переносное. Оставшееся движение – вращение точки вместе с кривошипом
– движение переносное. Оставшееся движение – вращение точки вместе с кривошипом 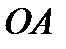 – движение абсолютное.
– движение абсолютное.
Абсолютная скорость точки 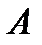
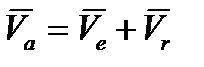 . (3.11)
. (3.11)
Определяем абсолютную скорость
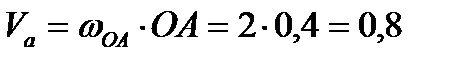 м/с.
м/с.
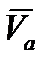 направлена
направлена 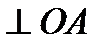 в сторону вращения
в сторону вращения 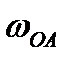 . Строим параллелограмм скоростей, чтобы
. Строим параллелограмм скоростей, чтобы 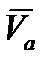 была его диагональю, одна из сторон направлена по
была его диагональю, одна из сторон направлена по 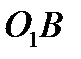 , вторая перпендикулярна ей (рис. 42).
, вторая перпендикулярна ей (рис. 42).
| x1 |
| Рис. 42 |
 Из треугольника скоростей
Из треугольника скоростей
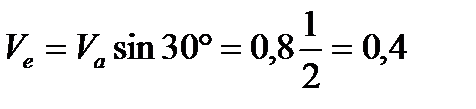 м/с,
м/с,
 м/с,
м/с,
тогда 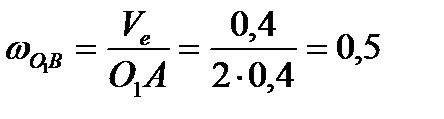 рад/с.
рад/с.
| y1 |
 . Записываем выражение для абсолютного ускорения точки
. Записываем выражение для абсолютного ускорения точки 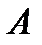
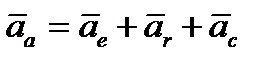 . (3.12)
. (3.12)
Или с учётом вида абсолютного, переносного и относительного движений
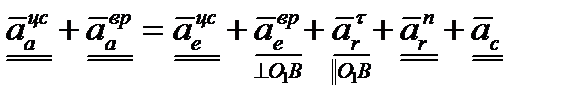 . (3.13)
. (3.13)
Составляющие абсолютного ускорения, подчеркнутые в векторном равенстве (3.13) двумя чертами, известны по модулю и направлению, одной чертой – только по направлению.
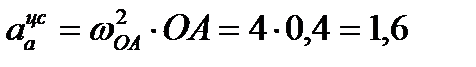 м/с²,
м/с², 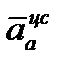 направлен по
направлен по 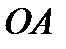 ;
;
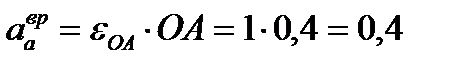 м/с²,
м/с², 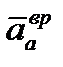 направлен
направлен  в сторону
в сторону 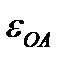 ;
;
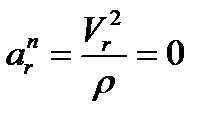 , так как относительное движение – прямолинейное, значит
, так как относительное движение – прямолинейное, значит 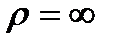 ;
;
 м/с², направлен по
м/с², направлен по 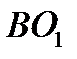 , от B к O1.
, от B к O1.
Ускорение Кориолиса 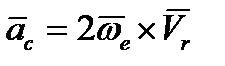 .
.
По модулю 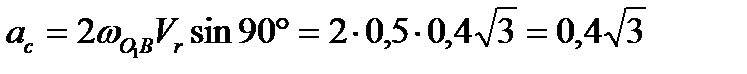 м/с².
м/с².
Используя правило Жуковского, указываем направление вектора 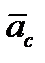 . Задаём направления ускорений
. Задаём направления ускорений 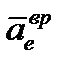 (перпендикулярно
(перпендикулярно 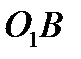 ) и
) и 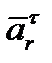 (по
(по 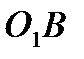 ) (рис. 42).
) (рис. 42).
Проектируем векторное равенство (3.13) на ось 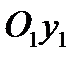
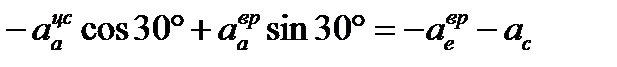 .
.
Отсюда
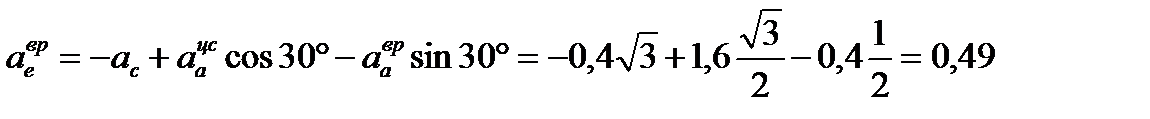 м/с².
м/с².
Так как 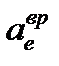 получилось со знаком «+», то на рис. 42 указано верное направление вектора
получилось со знаком «+», то на рис. 42 указано верное направление вектора 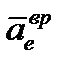 .
.
Тогда угловое ускорение кулисы O1B равно:
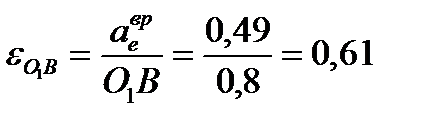 рад/с².
рад/с².
Ускорение  направлено в сторону, куда
направлено в сторону, куда 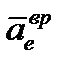 вращает кулису вокруг оси O1.
вращает кулису вокруг оси O1.
Проектируя векторное равенство (3.13) на ось 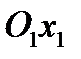 , можно найти относительное ускорение
, можно найти относительное ускорение 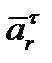 .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое сложное движение точки?
2. Что называется относительным, переносным и абсолютным движением?
3. Как определяется скорость точки при сложном движении?
4. Как определяется ускорение точки при сложном движении?
5. В каких случаях при сложном движении точки ускорение Кориолиса равно нулю?
Дата добавления: 2016-03-15; просмотров: 2251;
