Частный случай приведения плоской системы сил
К одному центру
При приведении плоской произвольной системы сил к произвольному центру О получаем одну силу 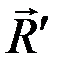 , равную геометрической сумме сил системы и называемую главным вектором системы сил
, равную геометрической сумме сил системы и называемую главным вектором системы сил
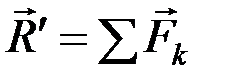 , (2.18)
, (2.18)
и одну пару 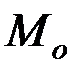 , называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О:
, называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О:
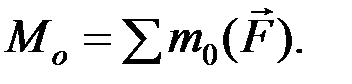 (2.19)
(2.19)
Модуль 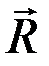 главного вектора
главного вектора 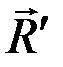 плоской системы сил определяется по его двум проекциям на оси координат
плоской системы сил определяется по его двум проекциям на оси координат
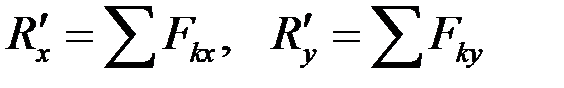 . (2.20)
. (2.20)
Тогда 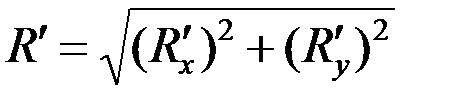 ,
,
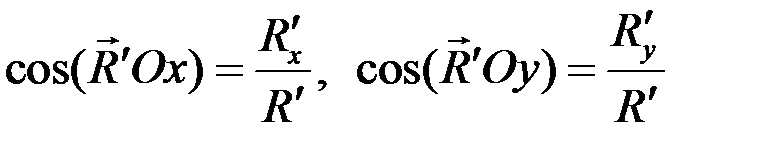 .
.
Частные случаи приведения плоской системы сил к одному центру:
1. 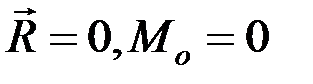 – система сил находится в равновесии.
– система сил находится в равновесии.
2. 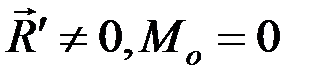 – система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
– система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
3. 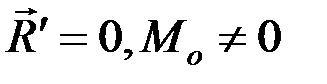 – система приводится к паре сил, момент которой не зависит от выбора центра приведения О.
– система приводится к паре сил, момент которой не зависит от выбора центра приведения О.
4. 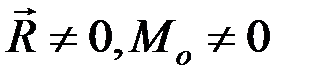 . Учитывая, что для плоской системы сил вектор главного момента
. Учитывая, что для плоской системы сил вектор главного момента 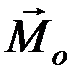 относительно любого центра приведения О всегда перпендикулярен
относительно любого центра приведения О всегда перпендикулярен 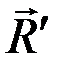 , т.е.
, т.е. 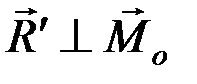 , этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (
, этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил ( 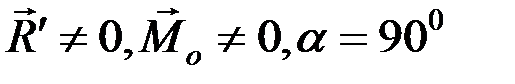 ), значит, в этом случае плоская система сил приводится к равнодействующей.
), значит, в этом случае плоская система сил приводится к равнодействующей.
Можно сделать вывод, что плоская произвольная система сил всегда приводится к равнодействующей, если не находится в равновесии (случай 1) и не приводится к одной паре (случай 3).
Дата добавления: 2016-03-15; просмотров: 1574;
