Условия равновесия пространственной и плоской

Систем сил

Для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы главный вектор системы 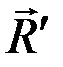и главный момент 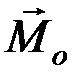относительно произвольного центра О равнялись нулю:

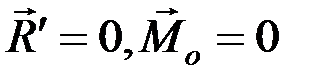. (2.21)

Геометрические условия равновесия (2.21) выражаются в замкнутости многоугольников сил и пар самих на себя.

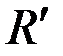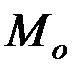При выполнении условий (2.21) модули и также равны 0. Из выражения (2.15) следует, что 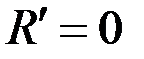, если каждое из слагаемых под радикалом в выражении (2.15) равно нулю. Аналогично 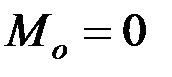, если каждое слагаемое под радикалом в выражении (2.17) равно нулю. Отсюда получаем шесть уравнений (2.22), характеризующих аналитические условия равновесия пространственной произвольной системы сил:

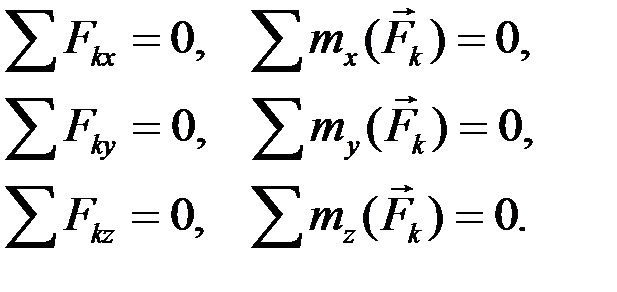(2.22)

Для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы суммы проекций сил на три координатные оси и суммы моментов сил относительно трех координатных осей равнялись нулю.

Если на тело действует пространственная система параллельных сил и система координатных осей Оxyz выбрана так, чтобы ось Oz была параллельна силам, то в этом случае из шести уравнений (2.22) три 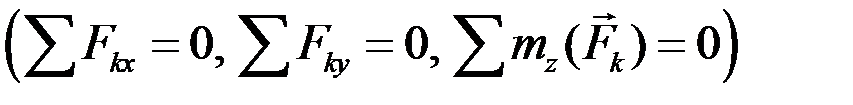обращаются в тождество 0=0 и выпадают. Остаются три уравнения, характеризующие условия равновесия пространственной системы параллельных сил:

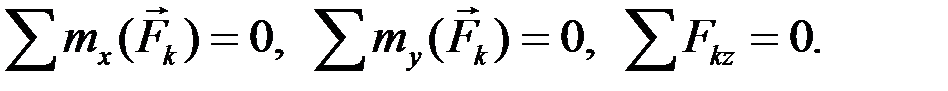(2.23)

Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма их проекций на ось, параллельную силам, и суммы моментов относительно двух других осей равнялись нулю.

Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы выполнялось условие

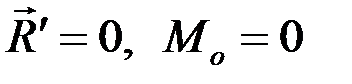. (2.24)

Из (2.20) следует, что модуль главного вектора 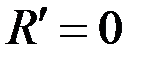, если каждая из двух его проекций равна нулю. С учётом выражений (2.19) и (2.20) получаем три уравнения (2.25), определяющие аналитические условия равновесия плоской произвольной системы сил:

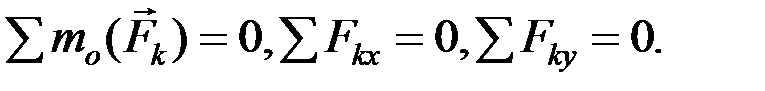(2.25)

Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы суммы их проекций на две координатные оси и сумма моментов всех сил относительно произвольной точки О равнялись нулю.

Если на тело действует плоская система параллельных сил и система координатных осей Oxy выбрана так, чтобы ось Оy была параллельна силам, то в этом случае в уравнениях (2.25) одно 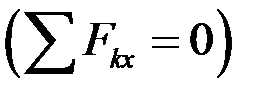обращается в тождество 0=0 и выпадает. Остаются два уравнения (2.26), определяющие условия равновесия плоской системы параллельных сил:

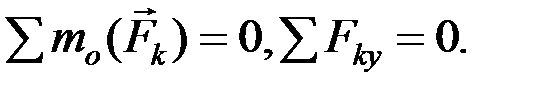(2.26)

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма их проекций на ось, параллельную силам, и сумма моментов всех сил относительно любой точки О равнялись нулю.

Кроме основной формы равновесия (2.25), для плоской произвольной системы сил существуют две дополнительные формы равновесия (2.27) и (2.28):

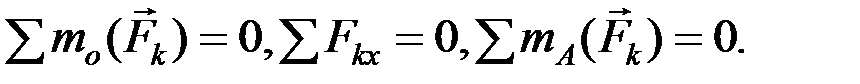(2.27)

Здесь ось Ox не должна быть перпендикулярна прямой ОА.

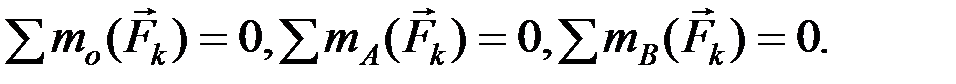(2.28)

Здесь моментные точки О, А, В не должны находиться на одной прямой.

Следует отметить, что для решения задач предпочтительнее основная форма равновесия плоской системы сил (2.25). На эту форму равновесия не накладываются никакие ограничения и её проще применять: два раза проектировать на оси и один раз составлять сумму моментов.