Теорема о приведении пространственной произвольной
системы сил к одному центру (основная теорема статики)
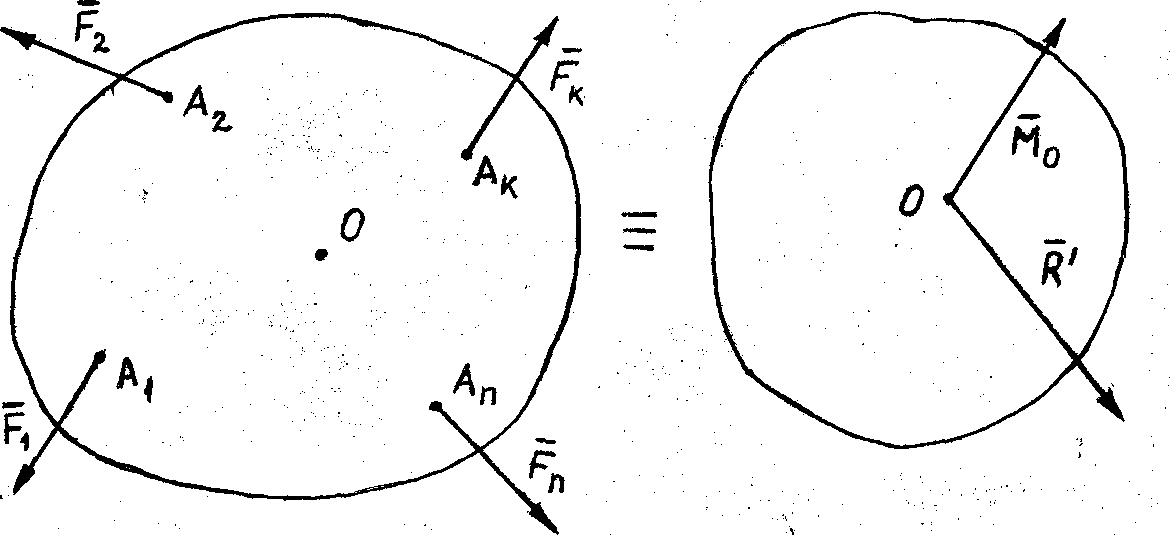
| Рис. 40 |
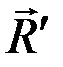, равную геометрической сумме всех сил и называемую главным вектором данной системы сил, и одну пару 
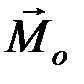, равную геометрической сумме моментов сил системы относительно центра приведения О и называемую главным моментом системы сил относительно центра приведения О.
Главный вектор 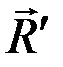и главный момент относительно центра приведения O 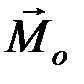пространственной произвольной системы сил 
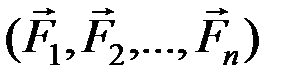(рис. 40) равны
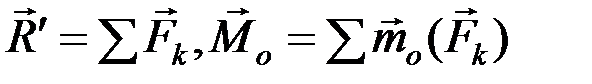. (2.13)
Модуль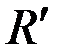 
главного вектора 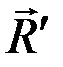системы сил определяется по его проекции на оси координат
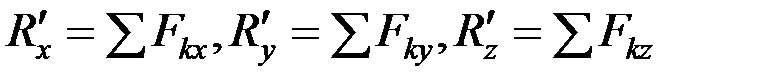. (2.14)
Зная проекции главного вектора, находим его модуль:
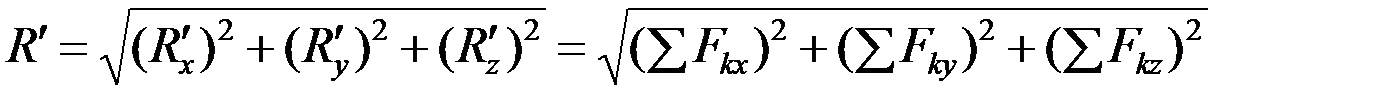(2.15)
и направляющие косинусы:
.
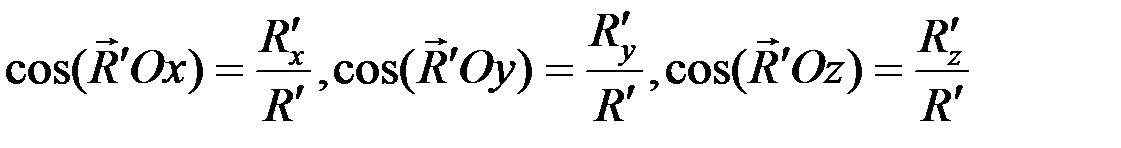Аналогично определяются проекции главного момента 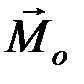относительно центра приведения О
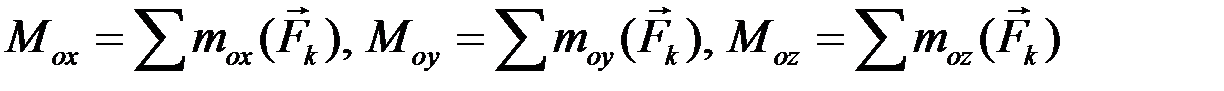.(2.16)
Тогда модуль главного момента равен
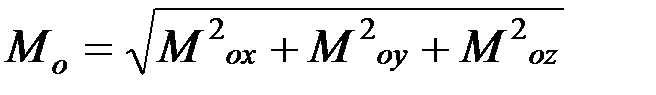. (2.17)
Направляющие косинусы вектора 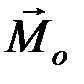равны
.
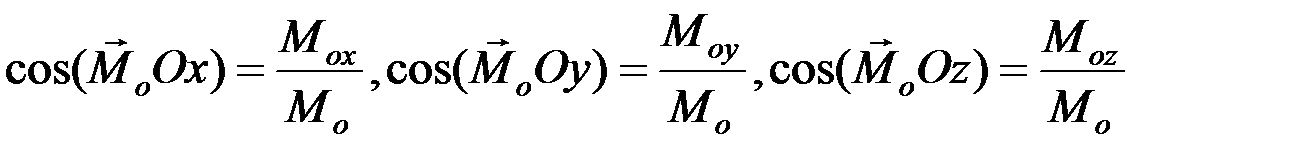Частные случаи приведения пространственной произвольной системы сил к одному центру О:
1. 
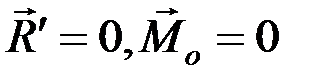– случай равновесия системы сил.
2. 
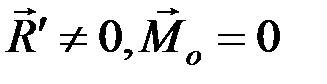– система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
3. 
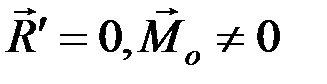– система приводится к одной паре, момент которой не зависит от выбора центра приведения.
4. 
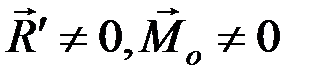и угол между ними 
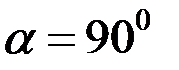– система приводится к равнодействующей.
5. 
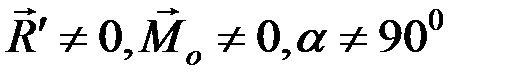– система приводится к динаме.
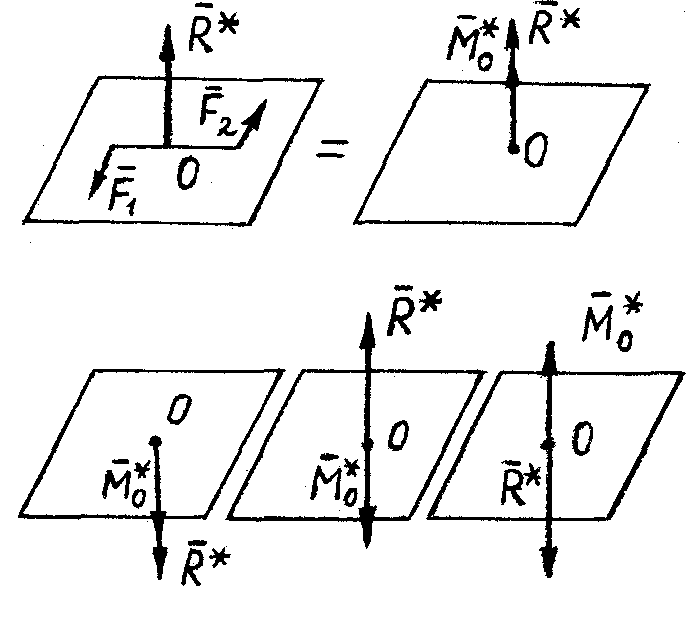
Динамой (силовым винтом) называется совокупность силы и пары, причем сила динамы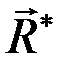 
перпендикулярна плоскости действия пары (рис. 41a).
Или иначе: динамой называется совокупность параллельных векторов силы 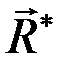и пары 
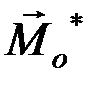(рис. 41б).
Если угол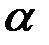 
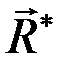между и 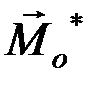равен 0, то силовой винт называется правым (рис. 41б,в), если = 
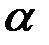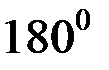, то силовой винт называется левым (рис. 41г,д).
| д) |
.
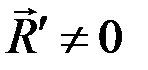| Рис. 41 |
| а) |
| б) |
| в) |
| г) |
| д) |
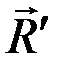и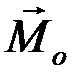 
, равен 0:
.
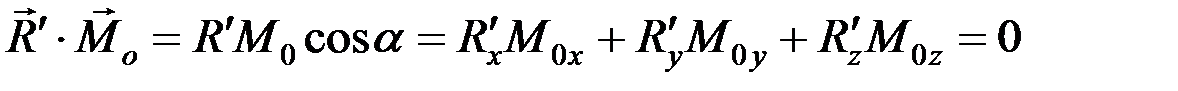Дата добавления: 2016-03-15; просмотров: 1032;