Графический метод расчета геометрического КЕО от светопроемов произвольной формы

Метод расчета основан на законе проекции телесного угла, в соответствии с которым:

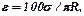% (70)

где s – проекция на освещаемую плоскость телесного угла W, под которым виден светопроем S из расчетной точки Т; R – радиус полусферы, в пределах которой измеряется телесный угол (рисунок 57).

Рисунок 45 –Схема к построению проекции телесного угла

Рассчитаем радиус круга из условия, что его площадь равна 40000 мм². В результате получим R » 113 мм. В соответствию зависимостью (70) значение e = 0,01 % создает светопроем S, проекция телесного угла, под которым он виден на освещаемую плоскость, составляет 4 мм². Исходя из этого, для расчета освещенности достаточно определить величину площади проекции телесного угла в полусфере радиусом R=113 мм и, зная, что ее площадь 4 мм² составляет 0,01 %, рассчитать освещенность.

Величина радиуса полусферы подобрана с учетом удобства измерения площади проекции телесного угла, для чего можно использовать миллиметровую бумагу с величиной ячейки 2´2 мм. В этом случае площадь проекции телесного угла s = 1 см² соответствует освещенности e » 0,25 %.

Для определения площади проекции телесного угла можно воспользоваться следующим способом. Допустим, есть разработанные в любом масштабе план, разрез, фасад и другие части проекта.

1. На условной рабочей поверхности (горизонтальная поверхность, размещенная на высоте 0,8 м от уровня чистого пола) или полу разместим расчетную точку Т и обозначим ее проекцию на плане через Т¢.

2. Из точки Т¢ как из центра проведем окружность радиусом 113 мм.

3. Выберем произвольную точку (А) на контуре светопроема и соединим ее прямой линией с точкой Т.

4. К проекции Т¢А¢ линии ТА на плане помещения из точки А¢. Проведем перпендикуляр и отложим на нем превышение точки А над освещаемой плоскостью.

5. Через полученную точку А¢¢ и точку Т¢ проведем прямую линию до встречи с окружностью и из точки встречи опустим перпендикуляр до линии Т¢А¢.

В результате получим проекцию a точки встречи линии ТА с поверхностью полусферы, то есть первую точку проекции телесного угла на освещаемую плоскость.

Аналогично следует определить достаточное количество проекций точек встреч с поверхностью полусферы линий, проведенных через контур светопроема и расчетную точку. Соединив полученные проекции точек плавной кривой, получим фигуру проекции на освещаемую плоскость телесного угла, под которым виден светопроем из расчетной точки.

Скопируем полученную фигурку на кальку и, наложив ее на миллиметровую бумагу (ячейки 2 мм), определим площадь, а затем – освещенность (можно строить фигуру проекции телесного угла на кальке, наложив ее на план).

Тема 10 Инсоляция

Общие положения

Инсоляция (от лат. insolare – выставлять на солнце) – совокупность воздействий на человека и окружающую среду солнечной радиации, проявляющихся в различных формах, например, в нагреве поверхности земли, воды, воздуха, отдельных зданий, а так же психологическом воздействии на человека, активном влиянии на биосферу земли и т.п. Под термином инсоляции следует понимать суммарное солнечное облучение, то есть облучение прямыми солнечными лучами, рассеянным светом неба и отраженным светом от различных формирований.

В архитектуре инсоляция является одним из определяющих условий формирования различных качеств объекта. В частности, для здания – это формирование внешнего вида, сочетание с окружающей средой, создание комфортных условий для людей. С учетом требований к инсоляции проектируют и застраивают города, размещают здания на генплане, подбирают их конструкции, решают объемно-планировочные вопросы, проектируют инженерно техническое оборудование.

Зодчие древности хорошо знали закономерности инсоляции отдельных зданий и городских ансамблей и учитывали их в своих работах. Например, античные города Египта имеют сетку улиц с отклонением от меридиана в пределах 40 – 60°, что позволяет обеспечивать наиболее равномерную инсоляцию города в течении года.

Для архитектора понимание существа инсоляции является необходимым условием. Это особо актуально в настоящее время в связи с энергетическими и экологическими проблемами, а так же с тем, что качество архитектуры определяется прежде всего комфортностью среды, надежностью конструкций, выразительностью пространств и форм и экономичностью проекта. Каждый из этих показателей качества архитектуры зависит от рационального решения вопросов инсоляции и солнцезащиты зданий и городских ансамблей. Здесь хотелось бы обратить внимание на то, что даже выдающиеся мастера иногда недоучитывали в своем творчестве значение инсоляции и солнцезащиты. Например, хорошо известно всем архитекторам здание дворца конгресса в Бразилии (архитектор О. Нимейер). Здание очень эффектно, а прием резкого контраста форм и пластики применяют многие архитекторы, но применение сплошного остекления стен высотной доминанты для климатических условий Бразилии экономически не выгодно из-за большого расхода энергии для охлаждения воздуха помещений летом и подогрева – зимой.

Подобных примеров можно привести очень много, что характерно для застройки в последнее время. Обусловлено это низким уровнем знаний архитекторов в области инсоляции, недостаточной глубиной научных разработок проблемы, несовершенством нормирования инсоляции и тем, что многие архитекторы не задумываются о энергозатратах на архитектурный объект в будущем.

Идея о нормировании инсоляции возникла еще в XIX веке. Но и до настоящего времени еще есть ряд спорных вопросов и проблем при ее нормировании, расчете и оценке. В нашей стране считают, что инсоляция играет важную роль в борьбе с болезнетворными бактериями и основным показателем нормируется продолжительность инсоляции. Некоторые зарубежные ученые доказывают, что роль инсоляции в этом процессе незначительна. Например, англичане пришли к выводу, что солнце играет важную роль только как фактор связи с внешним миром и это в инсоляции основное, а ее продолжительность они считают второстепенным фактором. Необходимо учитывать не только положительные ее воздействия, но и отрицательные. Некоторые из положительных и отрицательных воздействий инсоляции приведены в таблице 11.

Таблица 11