Емкостное сопротивление обратно пропорционально частоте и
величине емкости.
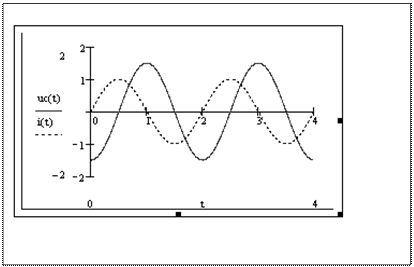
Емкостное напряжение отстает от тока по фазе на четверть периода (900).
Анализ последовательных R, L, C – цепей при гармоническом
воздействии
1. Анализ последовательной RL-цепи
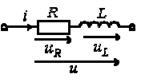
На основе второго закона Кирхгофа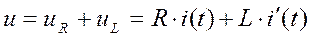 
.
Приведем уравнение в комплексную форму на основе того, что частота тока и напряжения будет одна и та же.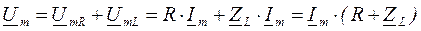 
Получим алгебраическое выражение:
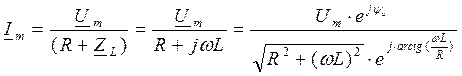. Здесь 
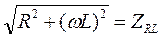- полное сопротивление последовательной RL-цепи; а 
- комплексное сопротивление RL цепи. При частоте ω=0 ZRL(0)=R, при ω=∞ ZRL(∞)=∞.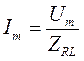 
, тогда Im(0)= Um/R и Im(∞)=0.
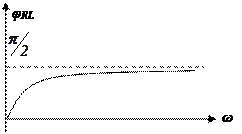
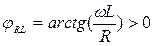- угол сдвига фаз между напряжением и током в RL-цепи. В последовательной RL-цепи напряжение опережает ток на угол меньше чем 900 , φ(0)=0 φ(∞)=π/2 .
.
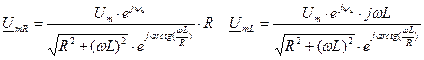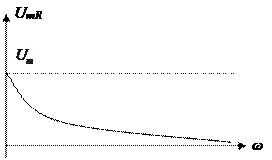
UmR(0)=Um, UmR(∞)=0.
Частотные характеристики последовательной RL цепи при Um=const.
| |
| |
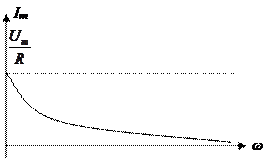
UmR(0)= Um, UmR(∞)=0
UmL(0)= 0, UmL(∞)=Um
| |
| |
Для наглядности строят треугольник сопротивлений и векторную диаграмму
Рассмотрим это для последовательной RL-цепи. При этом отрезок, соответствующий резистивному сопротивлению, откладывают по горизонтали, а индуктивному сопротивлению из конца этого отрезка вертикально вверх. В этом случае образуется прямоугольный треугольник, где гипотенуза соответствует полному сопротивлению RL – цепи.
Совокупность нескольких векторов, отображающих токи и напряжения в некоторой цепи, называется векторной диаграммой. При построении векторной диаграммы сначала строится вектор тока Im со своим углом, затем вектор резистивного напряжения UmR под тем же углом, потом вектор индуктивного напряжения UmL из конца этого вектор под углом +900. В этом случае гипотенуза образованного прямоугольного треугольника дает вектор общего напряжения Um.
, 
.
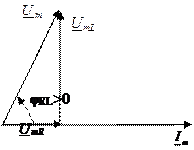
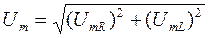Дата добавления: 2016-03-15; просмотров: 926;